Question

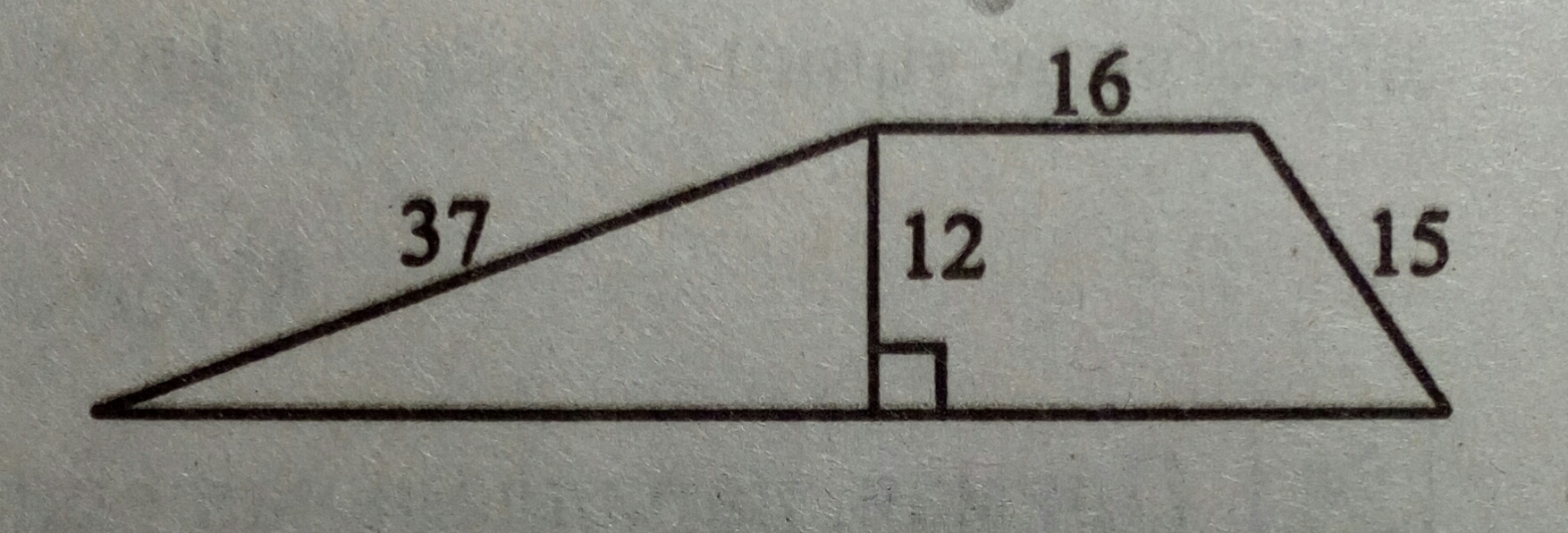
Найдите площадь трапеции изображённой на рисунке

Answer 1

Ответ:

$S_{ABCD}=456$

Пошаговое объяснение:

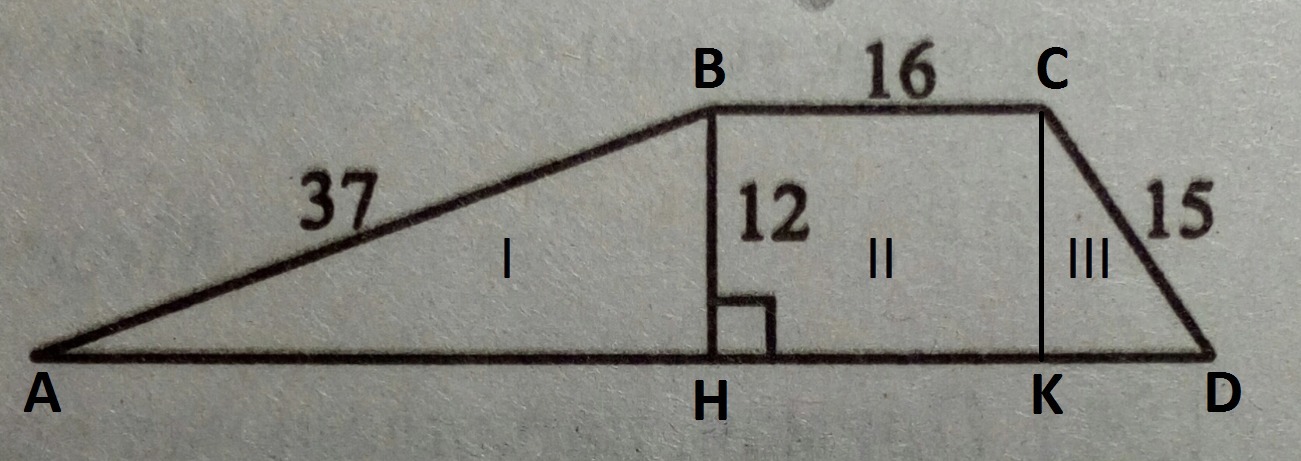
Введем обозначения. Проведем еще одну высоту CK в трапеции ABCD. Таким образом площадь трапеции равна сумме площадей двух треугольников ( ABH, CDK ) и прямоугольника ( BCKH ).

$1) S_{ABH}=\frac{1}{2}AH*BH$

AH вычислим по теореме Пифагора:

$AB^2=BH^2+AH^2\\AH=\sqrt{AB^2-BH^2}\\AH=\sqrt{1369-144}=35\\ S_{ABH}=\frac{1}{2}*35*12=210$

$2) S_{BCKH}=BC*CK\\S_{BCKH}=16*12=192$

$3) S_{CDK}=\frac{1}{2}KD*CK$

KD вычислим по теореме Пифагора:

$CD^2=KD^2+CK^2\\KD=\sqrt{CD^2-CK^2}\\KD=\sqrt{225-144}=9\\ S_{ABH}=\frac{1}{2}*9*12=54$

$S_{ABCD}=210+192+54=456$