Question

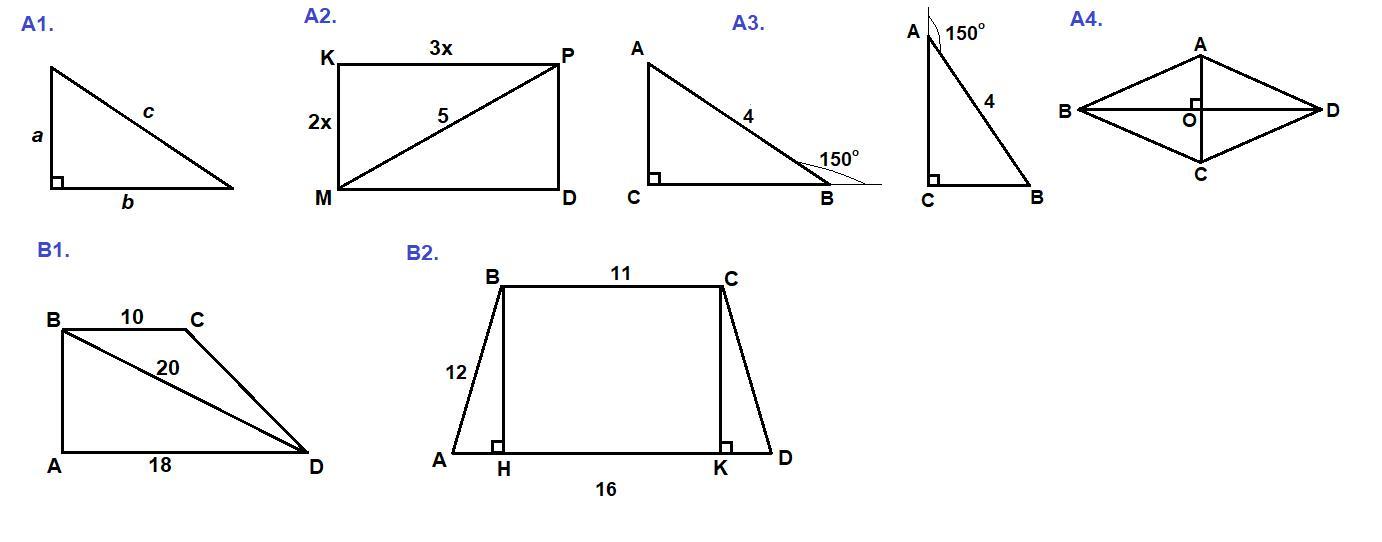
А1. Найдите гипотенузу прямоугольного треугольника, если его катеты равны 3см и 4см.


А2. Найдите меньшую сторону прямоугольника МКРД, если его смежные стороны относятся как 3:2, а диагональ равна 5см.



А3. Гипотенуза АВ прямоугольного треугольника АВС равна 4 см, а один из внешних углов равен 150 градусам. Найдите ВС.



А4. Найдите сторону ромба АВСД, если ВД= 8см и АС= 6см.



В1. В прямоугольной трапеции большая диагональ равна 20см, большее основание равно 18, меньшее основание равно 10см. Найдите площадь трапеции.




В2. Основания равнобедренной трапеции равны 11см и 16см, а боковая сторона – 12см. Найдите площадь трапеции.

ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО НАДО (С Решением)

Answer 1

Ответ:

А1.

а = 3 см

b = 4 см

По теореме Пифагора

c² = a² + b²

c = √(a² + b²) = √(3² + 4²) = √(9 + 16) = √25 = 5 см

А2.

Пусть х - одна часть, тогда

КР = 3х

МК = 2х

Из прямоугольного треугольника МКР по теореме Пифагора:

МК² + KP² = MP²

4x² + 9x² = 25

13x² = 25

x² = 25/13

x = 5/√13

MK = 2 · 5/√13 = 10/√13 = 10√13/13 см

А3.

Если внешний угол при вершине В равен 150°, то

∠АВС = 180° - 150° = 30°

$cos30^\circ=\dfrac{BC}{AB}$

$BC=AB\cdot cos30^\circ=4\cdot \dfrac{\sqrt{3}}{2}=2\sqrt{3}$ см

Если же внешний угол при вершине А равен 150°, то

∠ВАС = 180° - 150° = 30°

Тогда ВС - катет, лежащий против угла в 30°, значит равен половине гипотенузы:

ВС = АВ/2 = 4/2 = 2 см

А4.

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам:

АО = ОС = 6 : 2 = 3 см

BO = OD = 8 : 2 = 4 см

ΔАОВ:  ∠АОВ = 90°, по теореме Пифагора

АВ = √(АО² + ВО²) = √(9 + 16) = √25 = 5 см

В1.

ΔABD:  ∠BAD = 90°, по теореме Пифагора

АВ = √(BD² - AD²) = √(20² - 18²) = √(400 - 324) = √76 = 2√19 см

$S=\dfrac{AD+BC}{2}\cdot AB=\dfrac{18+10}{2}\cdot 2\sqrt{19}$

S = 14 · 2√19 = 28√19 см

В2.

Проведем ВН и СК - высоты.

ВНКС - прямоугольник, так как все углы прямые, значит

НК = ВС = 11 см

ΔАВН = ΔDCK по гипотенузе и катету (АВ = CD так как трапеция равнобедренная, ВН = СК как высоты трапеции)

АН = DK = (AD - HK)/2 = (16 - 11)/2 = 5/2 см

ΔАВН:  ∠АНВ = 90°, по теореме Пифагора

  ВН = √(АВ² - АН²) = √(12² - (5/2)²) = √(144 - 25/4) = √(551/4) = √551/2 см

$S=\dfrac{AD+BC}{2}\cdot BH=\dfrac{16+11}{2}\cdot \dfrac{\sqrt{551}}{2}=\dfrac{27\sqrt{551}}{4}$ см²