Докажите, что для произвольных множеств A, B и C справедливы следующие равенства:
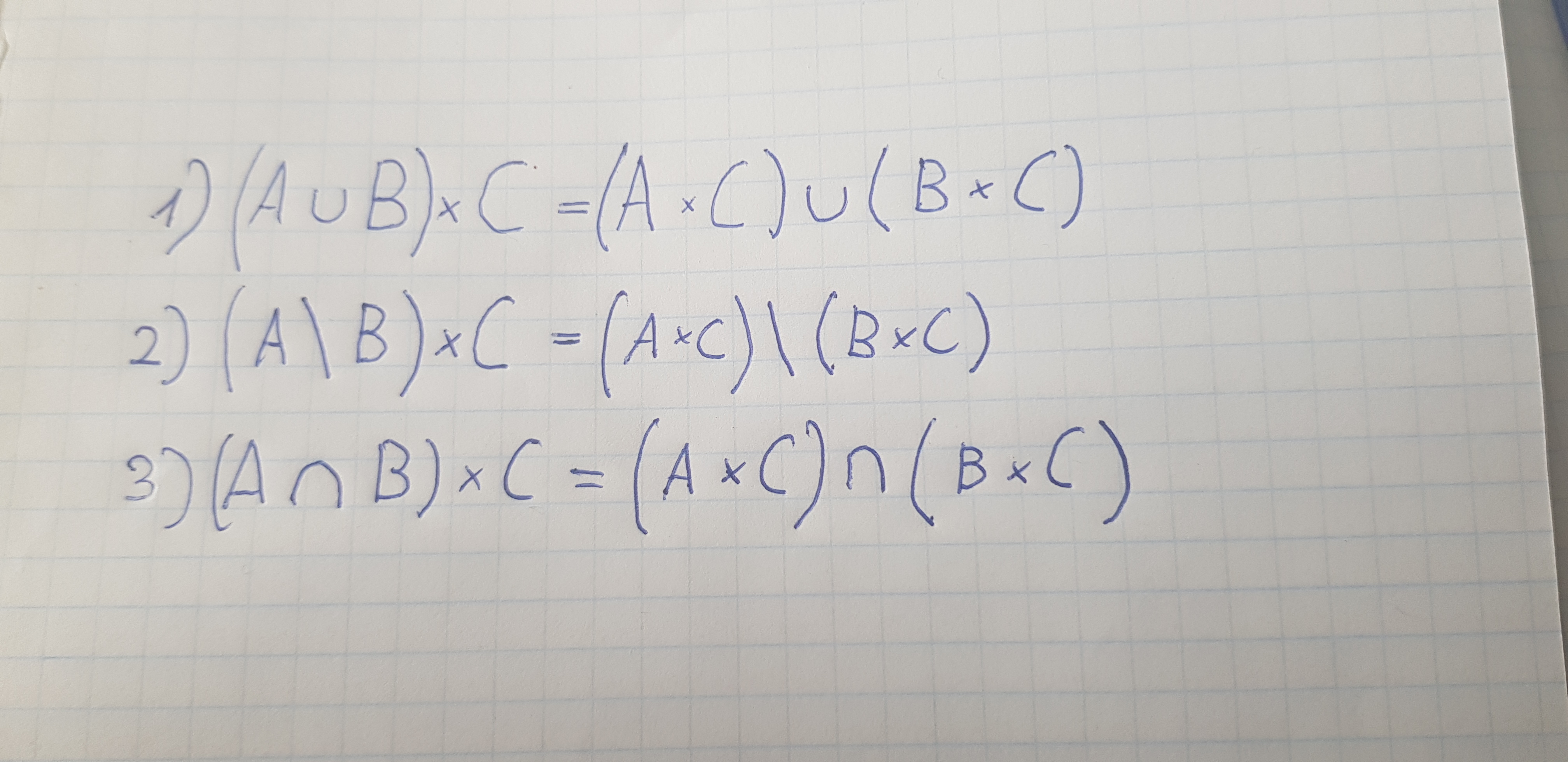
Ответы
Ответ:
Пошаговое объяснение:
Это Декартов произведения множеств
1.Пусть <x,y> є (AuB)xC<=>xє(AuB) и y є C<=>(xєA и yєC) или (xєB и yєC)<=>
<x,y>є(AxC)u(BxC)
2. <x,y>є(A\B)xC<=>(xєА и х не є B) и y єС <=> (xєА и yєС) и (x не єB и yєС)
Теперь нужно разобраться с этим (x не єB и yєС)
упорядоченная пара из двух элементов принадлежит Декартов Произведению множеств тогда,когда оба элемента принадлежат этим множеств,т.е,если оба элемента не принадлежат Декартов Произведения или хотя бы один из них не принадлежит Декартов Произведения,то тогда можно утверждать что данная упорядоченная пара не принадлежит Декартов Произведения множеств, следовательно
пара <x,y> не принадлежит (BxC)
Значит <x,y> є(AxC)\(BxC)
3. <x,y>є(A∩B)xC<=>(xєA и y єС) и (xєB и yєC). Мы вправе повторять yє C 2 раза, потому что смысл задачи не нарушается.
(xєA и y єС) и (xєB и yєC)<=><x,y>є(AxC) и <x,y>є(BxC)<=><x,y>є(AxC)∩(BxC)