Question

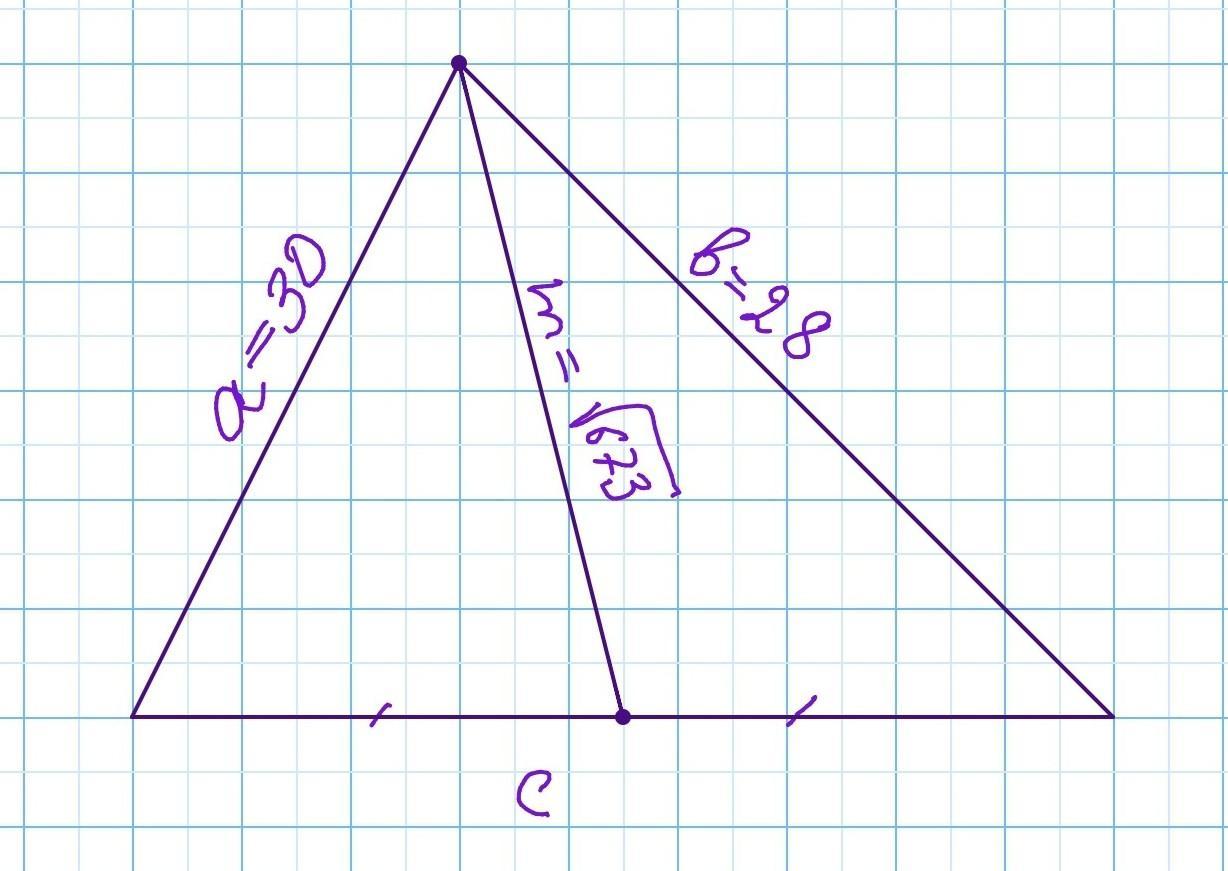
знайти площу трикутника, дві сторони якого дорівнюють 28 і 30 см, а медіана, яка проведена до третьої сторони дорівнює корінь з 673

Answer 1

Ответ:

336 кв.ед.

Объяснение:

Медиана разбивает треугольник на два равновеликих треугольника. Используя формулу Герона для нахождения площадей полученных равновеликих треугольников, выводится формула для нахождения медианы m:

$m = \frac{1}{2} \sqrt{2( {a}^{2} + {b}^{2}) - {c}^{2} }$

Находим с:

$2 \sqrt{673} = \sqrt{2( {30}^{2} + {28}^{2}) - {c}^{2} } \\ \\ 2 \sqrt{673} = \sqrt{2(900 + 784) - {c}^{2} } \\ \\ 4 \times 673 = 3368 - {c }^{2} \\ \\ {c}^{2} = 3368 - 2692 \\ \\ {c}^{2} = 676 \\ \\ c = \sqrt{676 } \\ \\ c = 26$

Находим полупериметр треугольника:

$p = \dfrac{a + b + c}{2} = \dfrac{30 + 28 + 26}{2} = 42$

По формуле Герона находим площадь треугольника: S△=

$= \sqrt{p(p - a)(p - b)(p - c)} = \\ \\ = \sqrt{42(42 - 30)(42 - 28)(42 - 26)} = \\ \\ = \sqrt{42 \times 12 \times 14 \times 16} = \sqrt{14 \times 3 \times 3 \times 4 \times 14 \times 16} = \\ \\ = 14 \times 3 \times 2 \times 4 = 336$

S△=336 ед²