Question

Постройте график функции y=cos(x-П/3)+1

Answer 1

Ответ:

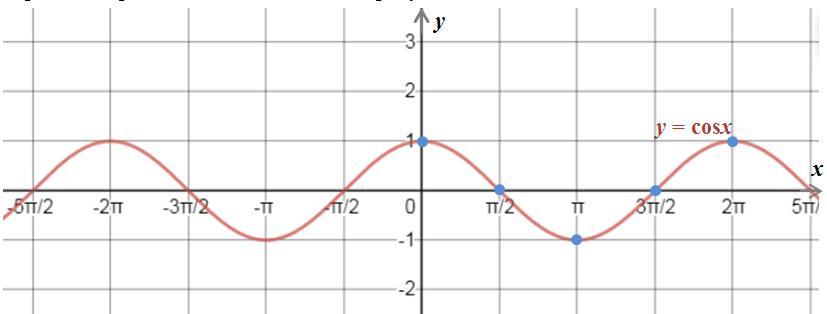
1) Построим основную часть графика функции y=cosx по ключевым точкам x=0; π/2; π; 3π/2; 2π:

y(0)=cos0=1;

y(π/2)=cosπ/2=0;

y(π)=cosπ= –1;

y(3π/2)=cos3π/2=0;

y(2π)=cos2π=1.

Учитывая тот факт, что период функции y=cosx равен 2π продолжим график влево и вправо копированием основной части (рисунок 1).

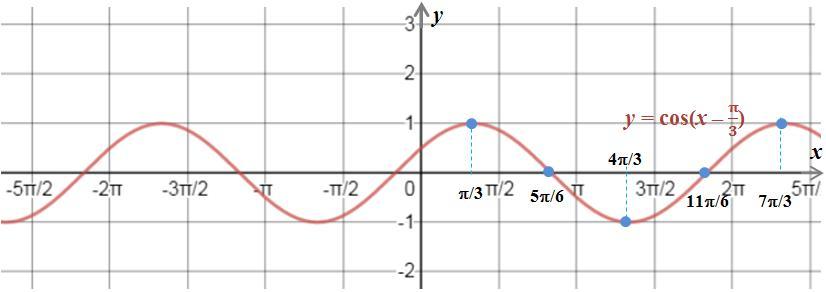
2) Получим график функции y=cos(x–π/3) сдвигом вправо по оси Ох ключевых точек на π/3 из графика функции y=cosx  (рисунок 2).  Нетрудно вычислить:

y(π/3)=cos(π/3–π/3)=cos0=1;

y(5π/6)=cos(5π/6–π/3)=cosπ/2=0;  

y(4π/3)=cos(4π/3–π/3)=cosπ= –1;

y(11π/6)=cos(11π/6–π/3)=cos3π/2=0;  

y(7π/3)=cos(7π/3–π/3)=cos2π=1.

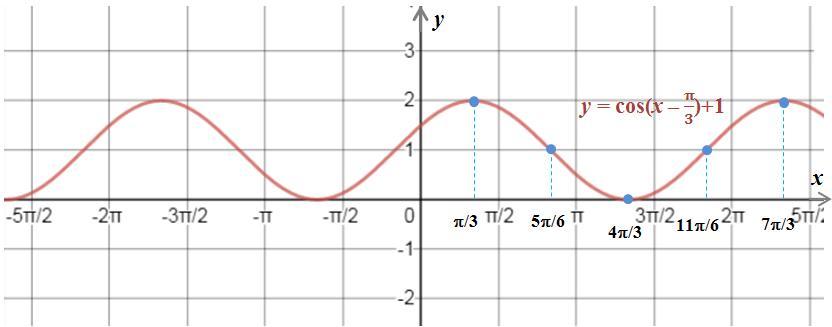
3) Получим график функции y=cos(x–π/3)+1 сдвигом на 1 единицу вверх из графика функции y=cos(x–π/3) (рисунок 3).  Легко вычислить:

y(π/3)=cos(π/3–π/3)+1=cos0+1=1+1=2;

y(5π/6)=cos(5π/6–π/3)+1=cosπ/2+1=0+1=1;  

y(4π/3)=cos(4π/3–π/3)+1=cosπ+1= –1+1=0;

y(11π/6)=cos(11π/6–π/3)+1=cos3π/2+1=0+1=1;  

y(7π/3)=cos(7π/3–π/3)+1=cos2π+1=1+1=2.