Question

В прямоугольном треугольнике с гипотенузой 12 найдите длину медианы, проведенной из вершины прямого угла

Answer 1

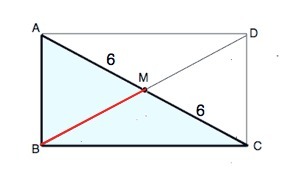
Обозначим треугольник АВС, угол В=90°. ВМ - медиана, ⇒АМ=СМ=6.

Достроим треугольник до прямоугольника ABCD. Проведем диагональ ВD. Диагонали прямоугольника равны  и точкой пересечения делятся пополам. Точка М - середина АС, она же делит диагональ ВD пополам. Половины диагоналей прямоугольника равны. 

⇒ВМ=АМ=СМ=6 (ед. длины)

-----------

Запомним это полезное свойство: Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.