Question

Решите задачу пожалуйста,завтра сдавать
за ранее спасибо большое

Answer 1

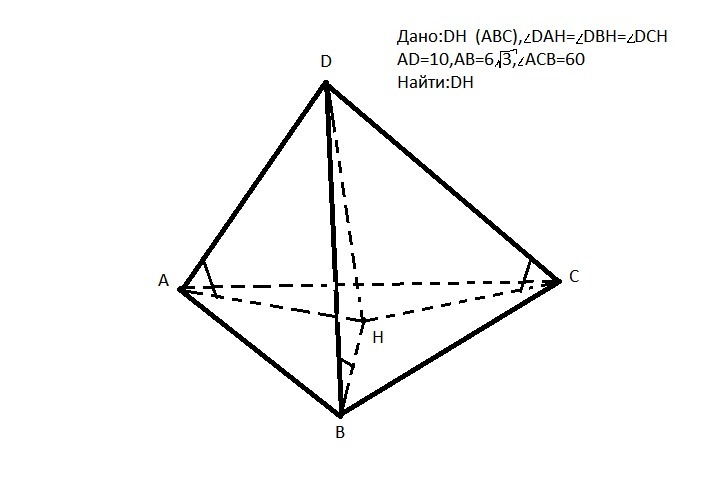
Прямоугольные треугольники DAH = DBH = DCH (сторона DH общая, углы равны по условию).

Следовательно AH = BH = CH и точка H является центром описанной окружности для ΔABC с радиусом R = AH = BH = CH

По теореме синусов:

$\frac{AB}{sinACB}=2R\\\frac{6\sqrt{3}}{\frac{\sqrt{3}}{2}}=2R\\R=6$

Из прямоугольного ΔADH по теореме Пифагора:

$DH^2=AD^2-AH^2=10^2-6^2=64\\DH=8$