Предмет: Математика,
автор: nbbc
Помогите найти производную
(x^3-7x+6)/(2x^3)
Дальше никак упростить не могу(
Приложения:
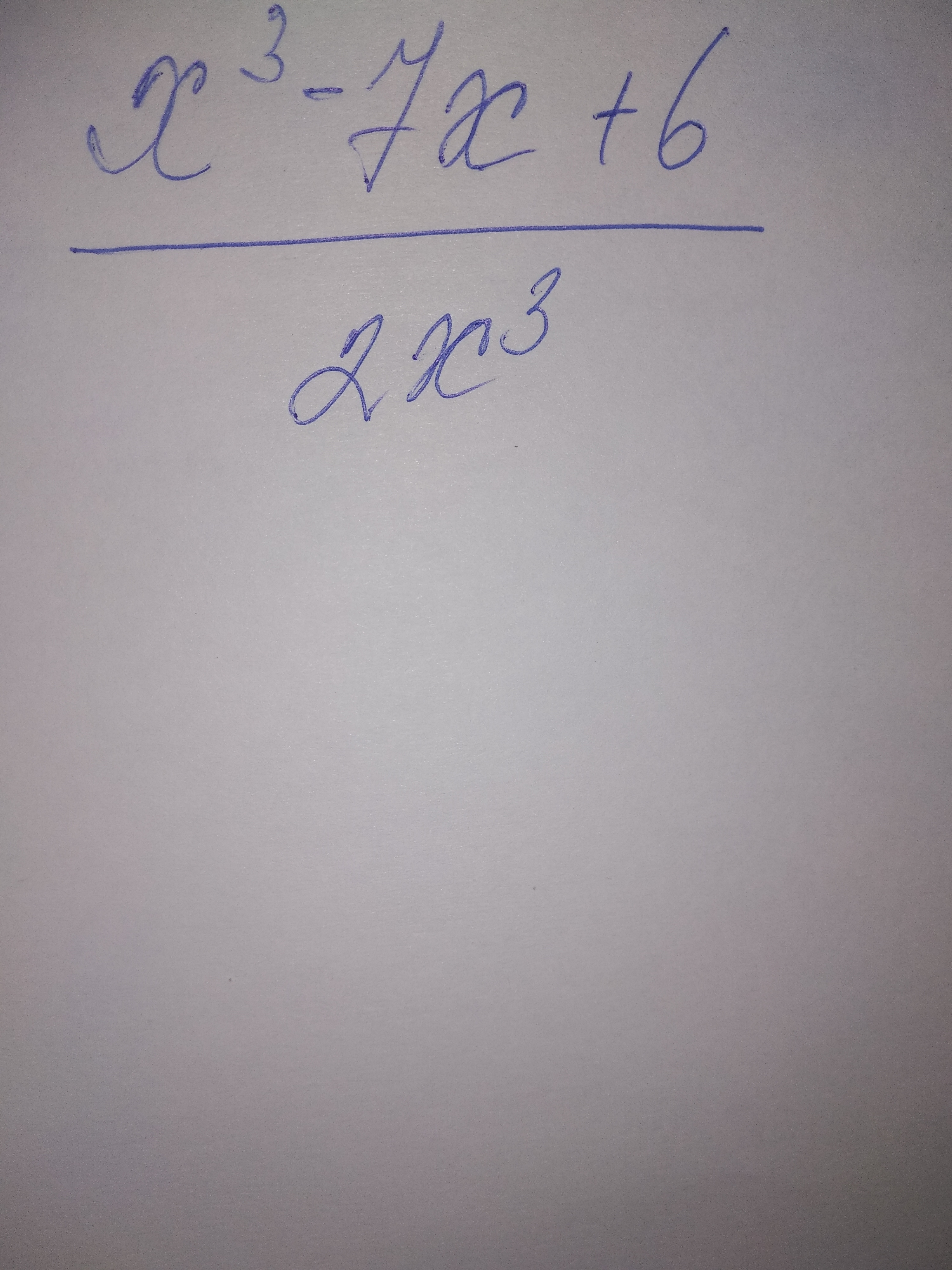
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Математика,
автор: bsslint
Предмет: История,
автор: asalya0990a
Предмет: Русский язык,
автор: bahha4141
Предмет: История,
автор: niDoSenhhkisabina
Предмет: Математика,
автор: stepafedorov9