Предмет: Алгебра,
автор: pozhiloyglad
Вычислить Tg если sin
если sin + cos
+ cos =
=
Ответы
Автор ответа:
1
sinx=sinx=2tg(x/2)/(1+tg^2(x/2))
cosx=(1-tg^2(x/2))/(1+tg^2(x/2))
sinx+cosx=sinx=2tg(x/2)/(1+tg^2(x/2))+(1-tg^2(x/2))/(1+tg^2(x/2))=√7/2
обозначу tg(x/2)=y
2y/(1+y^2)+(1-y^2)/(1+y^2)=(2y+1-y^2)/(1+y^2)=√7/2
-y^2+2y+1=√7/2+(√7/2)y^2
y^2(√7/2+1)-2y-1+√7/2=0
D=4-4(√7/2-1)(√7/2+1)=4-4(7/4-1)=4-3=1
y1=tg(x/2)=(2+1)/(√7+2)=3/(√7+2)
y1=tg(x/2)=(211)/(√7+2)=1/(√7+2)
Ответ tg(x/2)={3/(√7+2);1/(√7+2)}
Автор ответа:
1
...............................................................................................................................
Приложения:
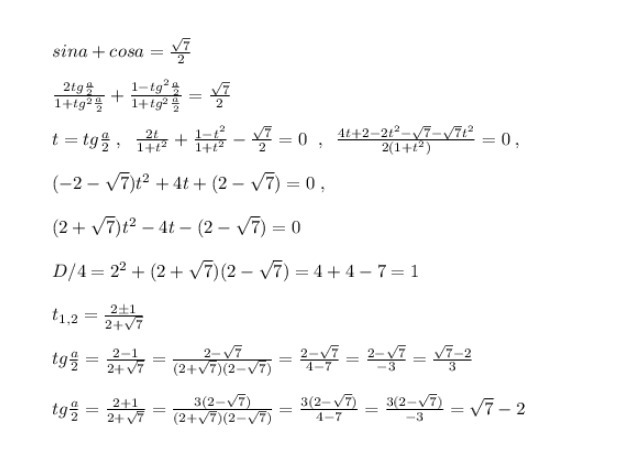
Похожие вопросы
Предмет: Физика,
автор: xwmc9bzpgt
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: nikolajbabenko582
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: baygubikov
https://znanija.com/task/30971656