Question

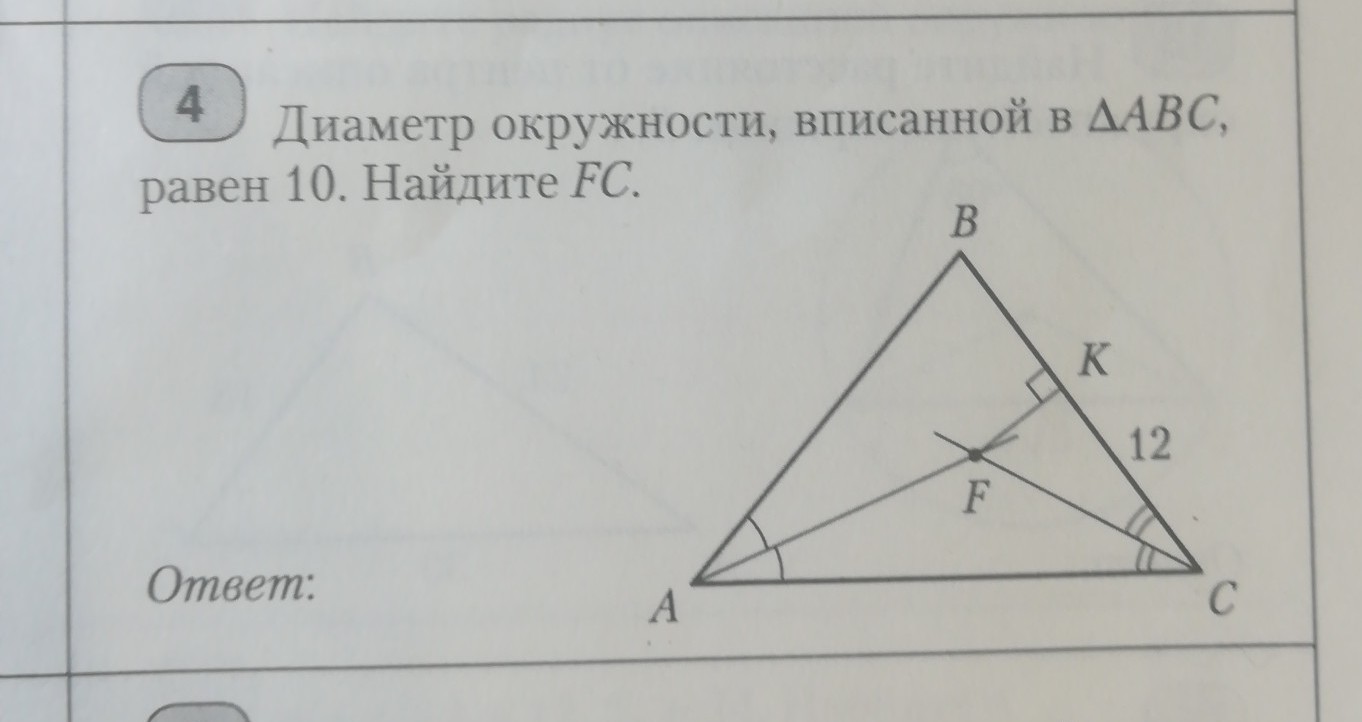
Диаметр окружности, вписанной в треугольник ABC равен 10. Найдите FC.

Answer 1

1) Высоту обозначим СН. Отрезки: АН=х;  BН=10-х.

Квадрат высоты, проведенной из вершины прямого угла треугольника равен произведению частей, на которые высота делит гипотенузу: СH^2=AH*BH;  9=x(10-x);  x=9.  AH=9см; BH=1см.

По теореме Пифагора, найдем катеты: АС=V90=3V10;  BC=V10.

2) В прямоугольном тр-ке радиус вписанной окружности равен половине разности между суммой катетов и гипотенузой: r=(a+b-c)/2;  r=(AC+BC-AB)/2=3V10+V10-10)/2=(4V10-10)/2=(2V10-5)см.

Задание 2.  

Площадь прямоугольного треугольника равна произведению полупериметра на радиус вписанной окружности: S=pr;  S=6*6=36(кв. см) .