Question

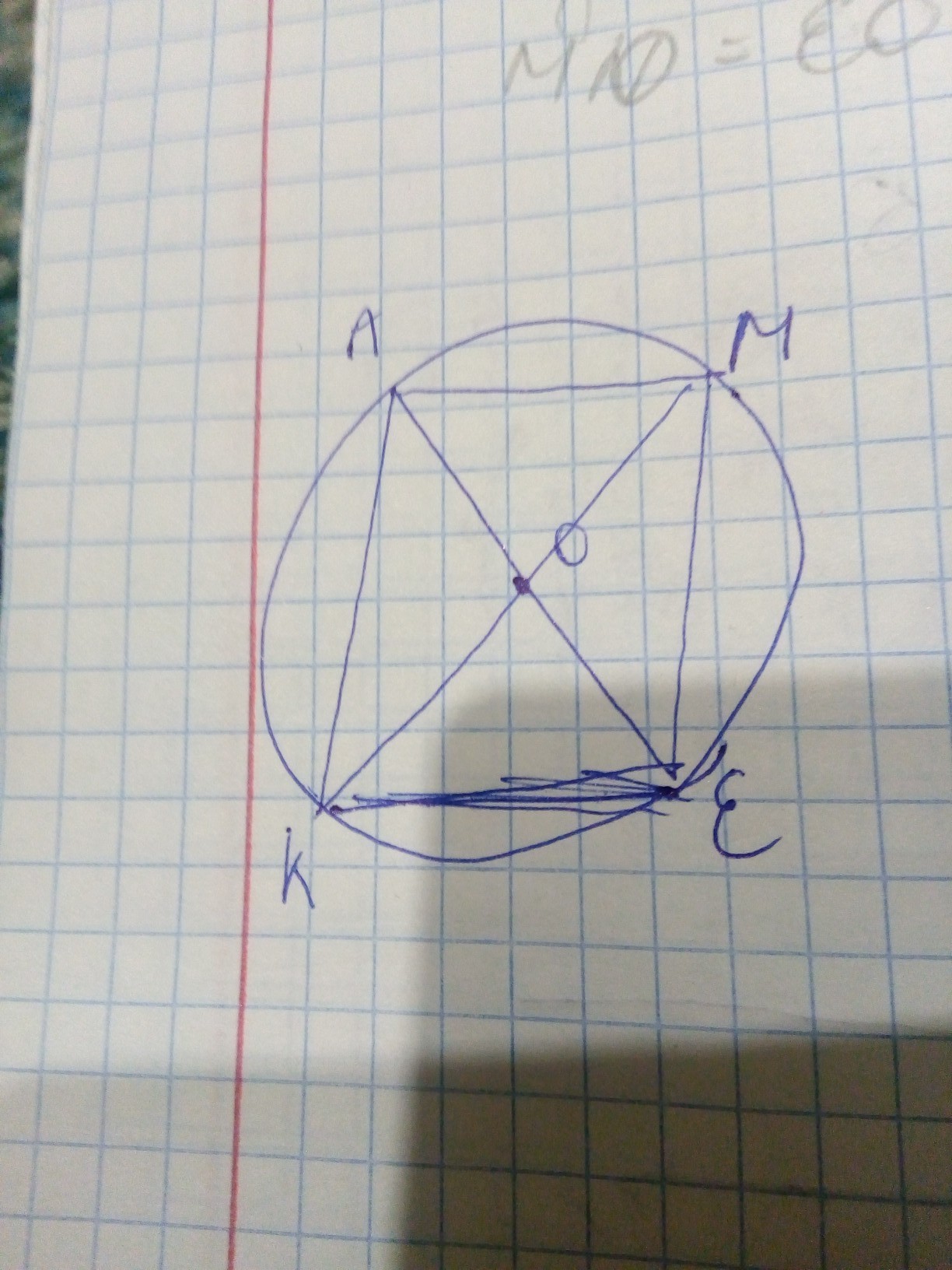
В окружности с центром O проведены диаметры KM и AE. Докажите, что: а) AK=EM; б) KE=AM; в)/_MKE=/_AMK.

Answer 1

Докажем,что AK=EM
Т.к по условию KM и AE диаметры ,то OK=AO=MO=EO(как радиусы),а углы AOK и MOE равны(как вертикальные)=> Треугольники AOK и MOE равны по двум сторонам и углу между ними=>AK=ME
Теперь докажем,что треугольники AOM и KOE равны. Углы AOM и KOE равны(как вертикальные),а ОКЕ=АМО и МАО=ОЕК(как накрест лежащие )=>треугольник АОМ равен треугольнику КОЕ по трём углам=>КЕ=АМ,а угол МКЕ равен углу АМК как накрест лежащие
Если не нравится доказательство в начале,то можно доказать аналогично тому,что во второй