Предмет: Алгебра,
автор: 6yxou
Помогите решить задачу по алгебре, очень надо.
Приложения:
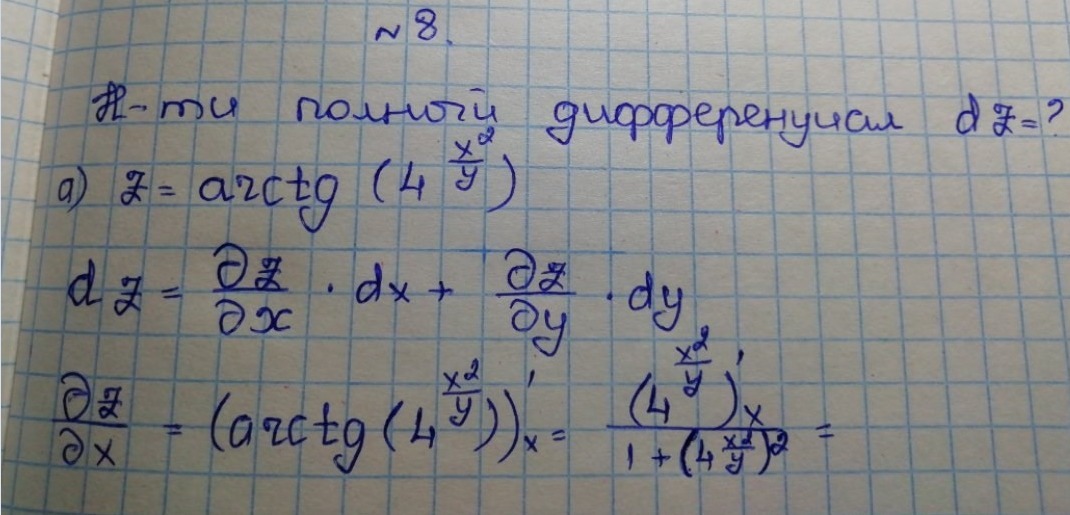
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: musaevhusejn44
Предмет: Литература,
автор: kirusha1007
Предмет: Другие предметы,
автор: timur070190
Предмет: Алгебра,
автор: нех