Предмет: Математика,
автор: yby24
Нужно сравните числа.
Приложения:
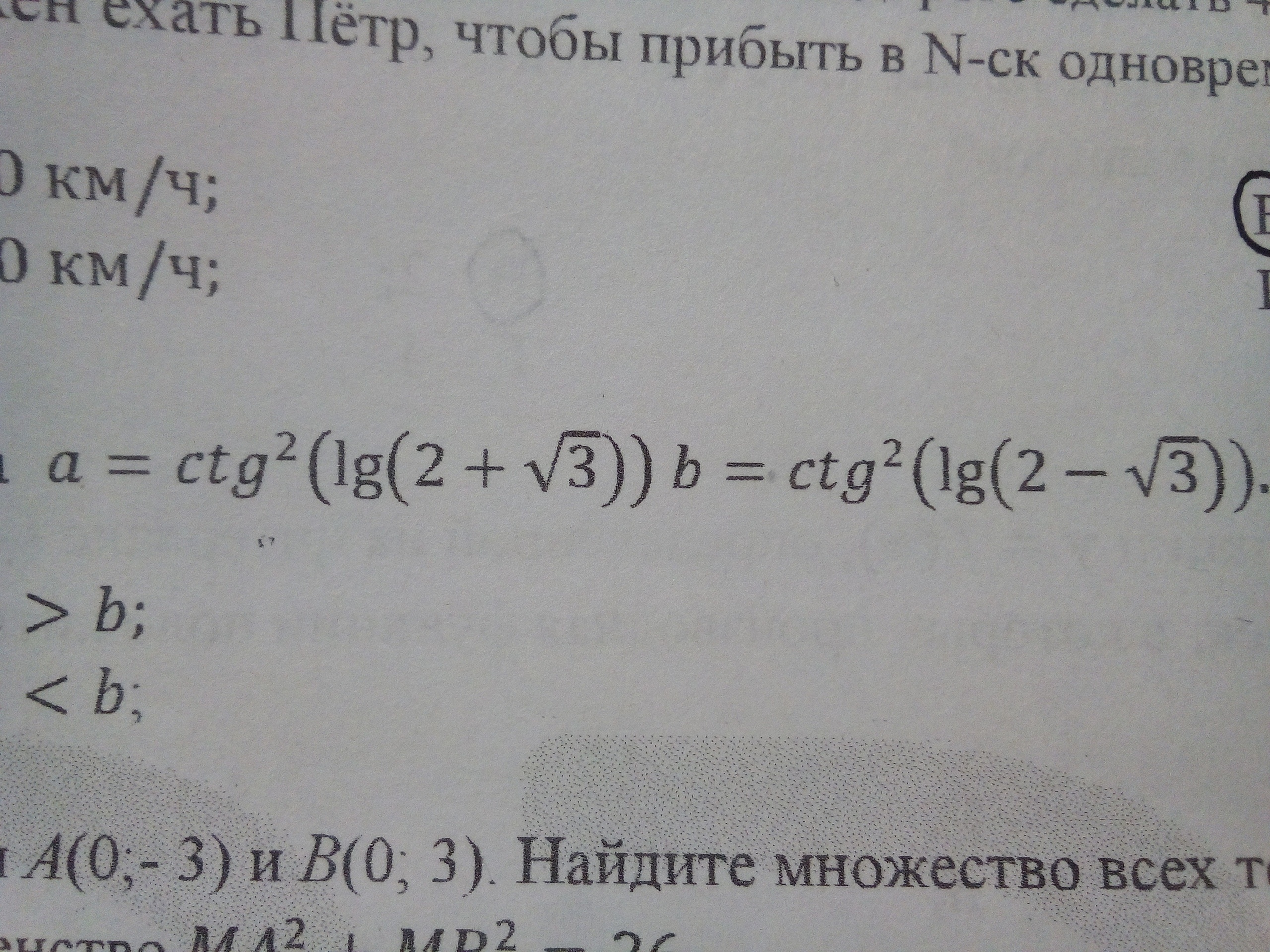
hote:
а=в. Есть такой вариант?
да
значит равноы
Ответы
Автор ответа:
3
Для начала заметим что числа а и в положительны, т.к. являются квадратами ctg.
Чтобы сравнить два положительных числа оценим их разность а-в
если а-в>0, то а>в
если а-в<0, то а<в
если а-в=0, то а=в
Что нам понадобится:
формула разности и суммы ctg
так же сумма и разность логарифмов (формула в общем виде)
теперь для упрощения преобразований я введу два угла
теперь решение
заметим что в знаменателе стоят положительные числа не равные нулю
вычислим синус разности и суммы углов
подставим в нашу разность чисел
Разность равна нулю, значит данные числа равны!
****************
можно проще
рассмотрим число а
числа а и в равны
Похожие вопросы
Предмет: Алгебра,
автор: viktoriakrotova16
Предмет: История,
автор: acerkavskij5
Предмет: Русский язык,
автор: sitkodima21
Предмет: Алгебра,
автор: 11lol22
Предмет: Математика,
автор: лера10101