Предмет: Математика,
автор: Натыовоаоаллв
Решить, Сроооооочно, 2 пример
Приложения:
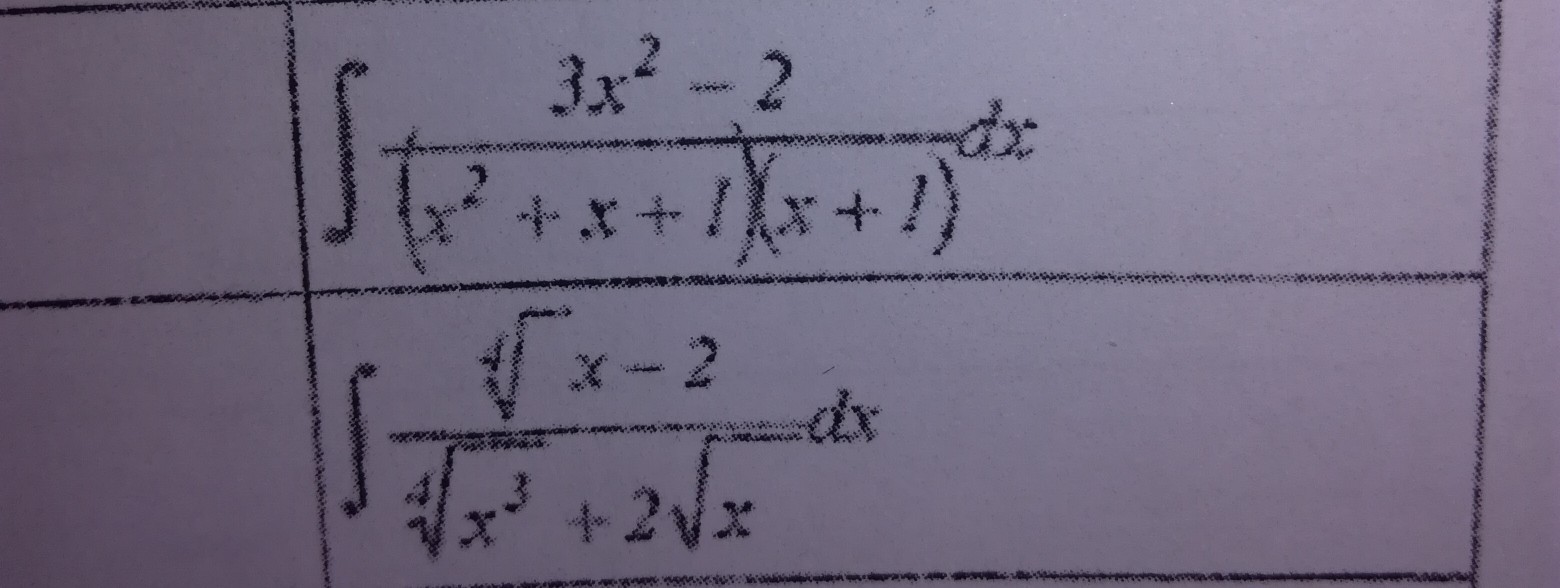
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: История,
автор: aydanibragimovna
Предмет: Қазақ тiлi,
автор: dobcinskaaolesa27
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: Ника100701