Question

на кривой y=x³+x²-7x+2 найдите точки, касательные которых паралельны прямой y=-2x+1

Answer 1

Пошаговое объяснение:

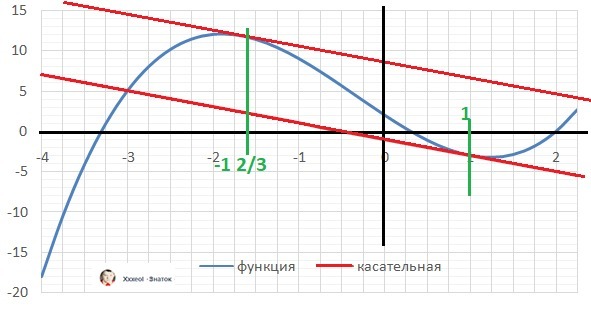
Уравнение касательной по формуле: y = F'(x)*(x - Xo) + F(Xo)

Касательная параллельна прямой с k = -2.

F'(x) = 3*x² - 2*x - 7 = - 2 -  одинаковый наклон. Решаем квадратное уравнение

3*x² - 2*x - 5 = 0,  D=64, √64 = 8,  x1 = 1, x2 = - 1 2/3

y(1) = - 3.0,  Дано: Точка A(1,-3), наклон  k = -2

b = Aу - k*Ax = -3 - (-2)*(1)  = - 1.

Уравнение прямой - Y(A) = -2*x -1  - касательная.

y(-1 2/3) ≈ 11.81

Дано: Точка В(-1,67,11,81), наклон  k = -2

b = Ву - k*Вx = 11,81 - (-2)*(-1,67)  = 8,48

Уравнение прямой - Y(В) = -2*x + 8,48  - касательная