Question

Написать уравнение прямой L1, проходящей через точку M0(1;-1) перпендикулярно к заданной прямой L1: -2x-3y+1=0

Answer 1

Пошаговое объяснение:

Преобразуем уравнение первой прямой к виду: y = k*x + b.

- 2x - 3y +1 = 0

3*y = - 2x +1

y = -2/3*x + 1/3 -  каноническое уравнение прямой.

k = - 2/3. У перпендикулярной прямой коэффициент наклона

k1 = - 1/k =  3/2 -  наклон перпендикуляра.

Находим сдвиг b.

b = Му - k*Мx = -1 - (1,5)*(1)  = -2,5

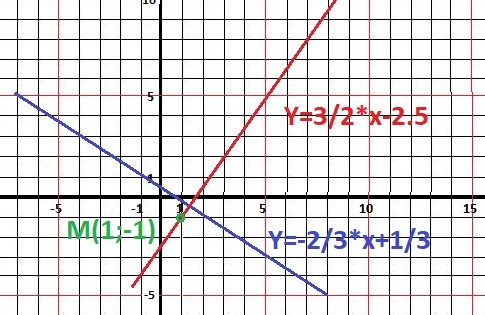
Уравнение прямой - Y(М) = 1,5*x - 2,5  - ответ.

Рисунок к задаче в приложении.