Предмет: Геометрия,
автор: dasew12
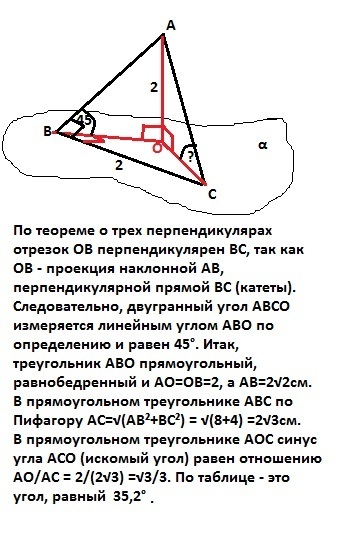
Катет BC прямоугольного треугольника ABC (∠ABC = 90°) лежит в плоскости α. Точка O — основание перпендикуляра, проведенного из вершины A к плоскости α. Двугранный угол ABCO равен 45°. Вычислите градусную меру угла между прямой AC и плоскостью α, если BC = 2 см, AO = 2 см.
Ответы
Автор ответа:
15
По теореме о трех перпендикулярах отрезок ОВ - проекция наклонной АВ, перпендикулярной прямой ВС (катеты). Следовательно, двугранный угол АВСО измеряется линейным углом АВО по определению и равен 45° (дано). Треугольник АВО прямоугольный и равнобедренный. Катеты АО=ОВ=2см, а гипотенуза АВ=2√2 см. В прямоугольном треугольнике АВС по Пифагору АС=√(АВ² +ВС²) = √(8+4) = 2√3см. В прямоугольном треугольнике АОС синус угла АСО (искомый угол, так как это угол между наклонной АС и плоскостью α по определению) равен отношению АО/АС = 2/(2√3) = √3/3. По таблице - это угол, равный 35,2°.
Ответ: 35,2°.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: SiKOkaDka
Предмет: Английский язык,
автор: esina4667
Предмет: Геометрия,
автор: rufatmasimov08
Предмет: Музыка,
автор: Мася203
Предмет: История,
автор: Ekaterinka0