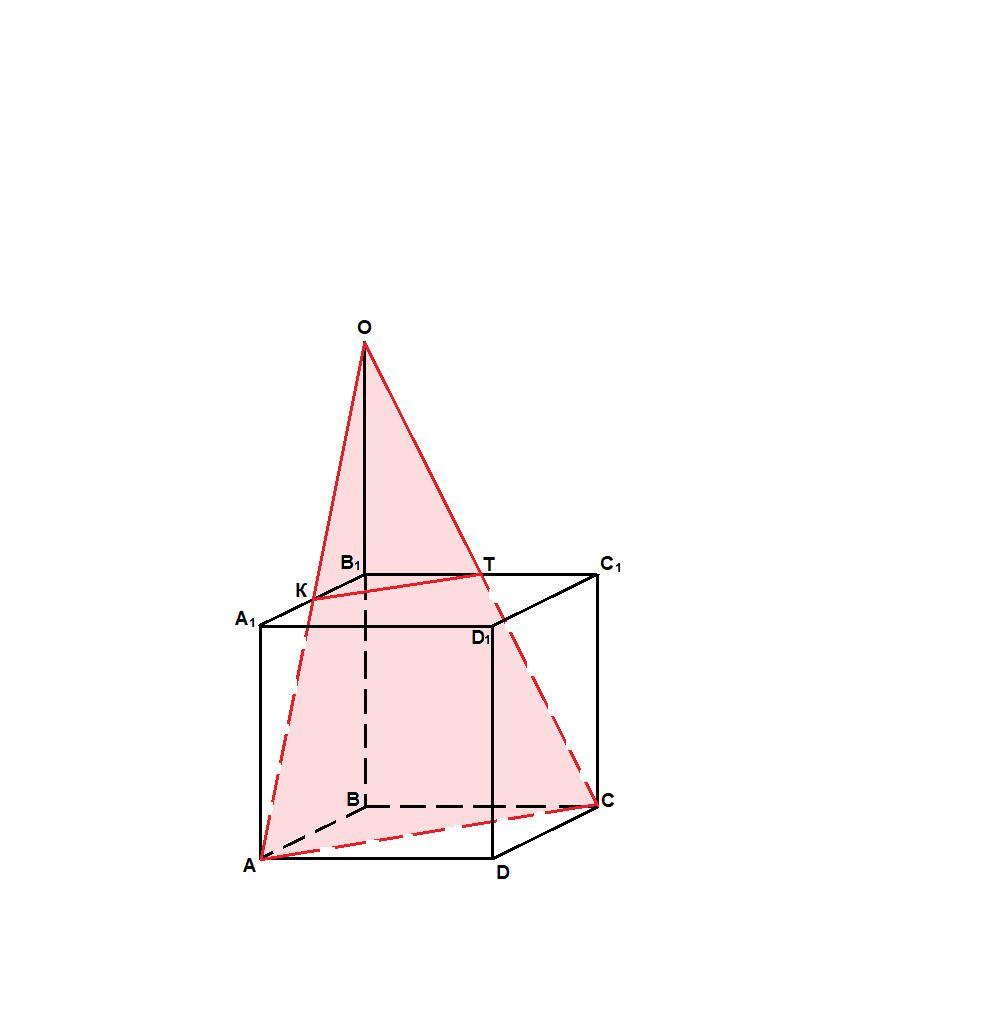
ABCDA1B1C1D1 — куб. Четырехугольник AKTC— сечение куба плоскостью, проходящей через вершины А, С и точку О такую, что точка B1 — середина отрезка ОВ. Докажите, что четырехугольник АKТС — равнобедренная трапеция, и вычислите длину ее средней линии, если длина ребра куба равна 2 см.
Ответы
Ответ:
1,5√2 см
Объяснения:
Точки А и О лежат в одной плоскости (АА₁В), проводим прямую АО, она пересечет ребро А₁В₁ в точке К.
Точки С и О лежат в одной плоскости (ВВ₁С), проводим прямую АС, она пересечет ребро В₁С₁ в точке Т.
АКТС - искомое сечение.
КТ ║ АС, так как параллельные плоскости (АВС) и (А₁В₁С₁) пересекаются плоскостью (АОС) по параллельным прямым.
АК ∦ ТС, так как эти прямые пересекаются в точке О,
значит АКТС - трапеция.
ΔАВО = ΔСВО по двум катетам (АВ = ВС как стороны квадрата, ВО - общий катет), значит
АО = ОС, ⇒ ΔАОС равнобедренный, ⇒
∠ОАС = ∠ОСА.
Но, если в трапеции углы при основании равны, то она равнобедренная, значит
АКТС - равнобедренная трапеция.
В ΔАОВ В₁ - середина ВО по условию, В₁К ║ ВА (лежат на противоположных сторонах квадрата), значит В₁К - средняя линия ΔАОВ, значит К - середина АВ.
КТ║АС, значит КТ - средняя линия ΔАОС.
АС = 2√2 см как диагональ квадрата,
КТ = АС / 2 = √2 см по свойству средней линии треугольника.
Средняя линия трапеции равна полусумме оснований:
m = (AC + KT) / 2 = (2√2 + √2) / 2 = 1,5√ 2 см