Предмет: Алгебра,
автор: nsundyrina
Найдите интервалы монотонности функции y=x³-3x
Ответы
Автор ответа:
1
у = х³ - 3х
у¹ = 3х² - 3
3х² - 3 = 0
х₁ = 1
х₂ = - 1
Это могут быть точки минимума и максимума функции.
Найдем значение производной на всех трех интервалах
х < -1 -1 < х < 1 и x > 1
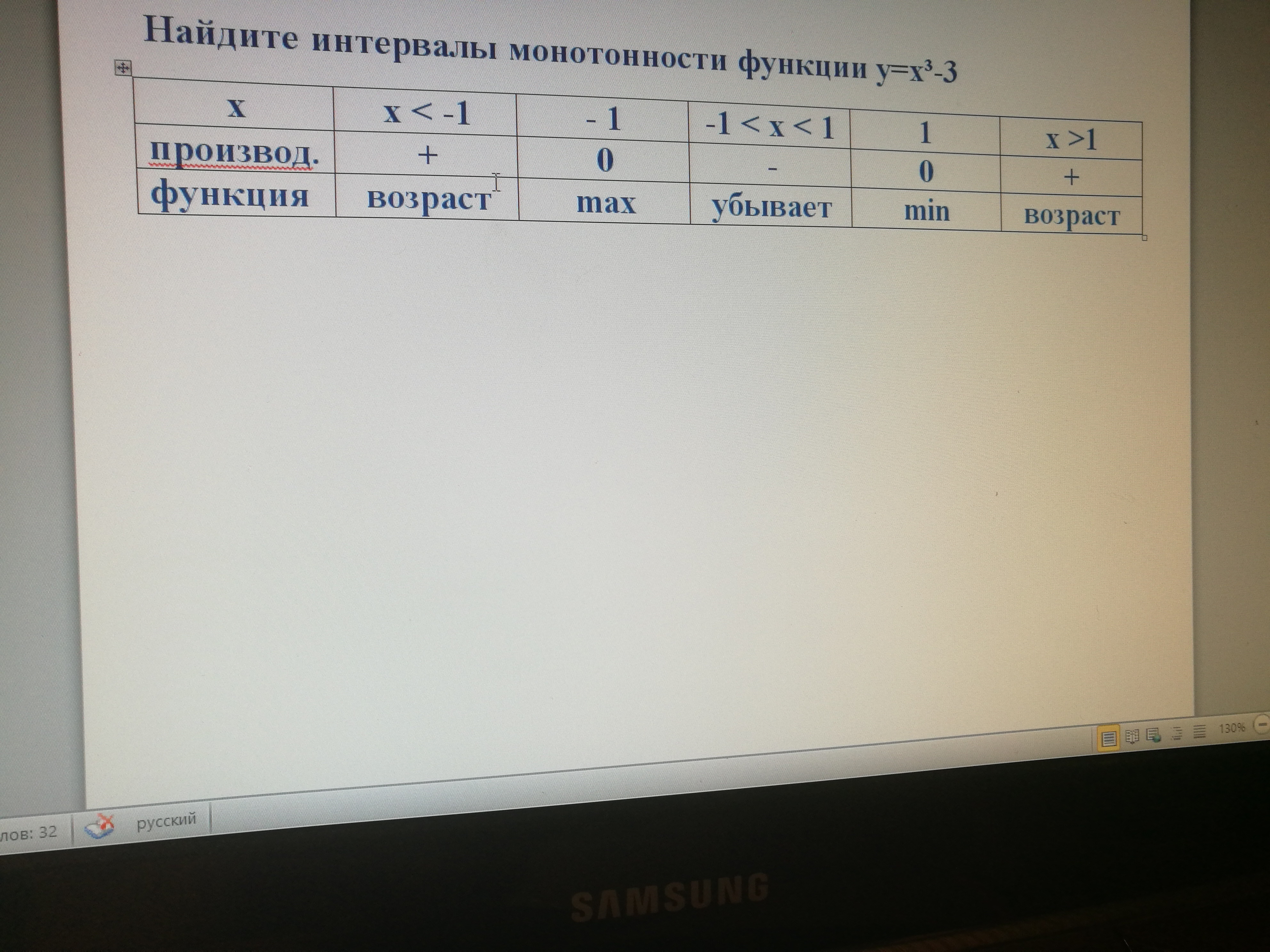
Внесем данные в таблицу (на фото).
Получим, на промежутке (-∞; -1) функция возрастает ,
На промежутке (- 1 ; 1) функция убывает
И на промежутке ( 1 ; + ∞) функция снова возрастает
в точке х= - 1 функция имеет максимум
в точке х = 1 функция имеет минимум.
Это и есть интервалы (или промежутки) монотонности функции
Приложения:
Похожие вопросы
Предмет: Литература,
автор: vk494kdqcq
Предмет: Информатика,
автор: tiktokpopkin
Предмет: Русский язык,
автор: mabd30358
Предмет: Математика,
автор: xiuschazorina2
Предмет: Литература,
автор: Оленька76