Предмет: Геометрия,
автор: washington2
Даю 30 баллов
найдите площадь четырехугольника если его диагонали взаимно перпендикулярны а их длины равны 5 и 11
Решите пожалуйста на листке, если можно, и чертеж с условиями
Ответы
Автор ответа:
14
Приложения:
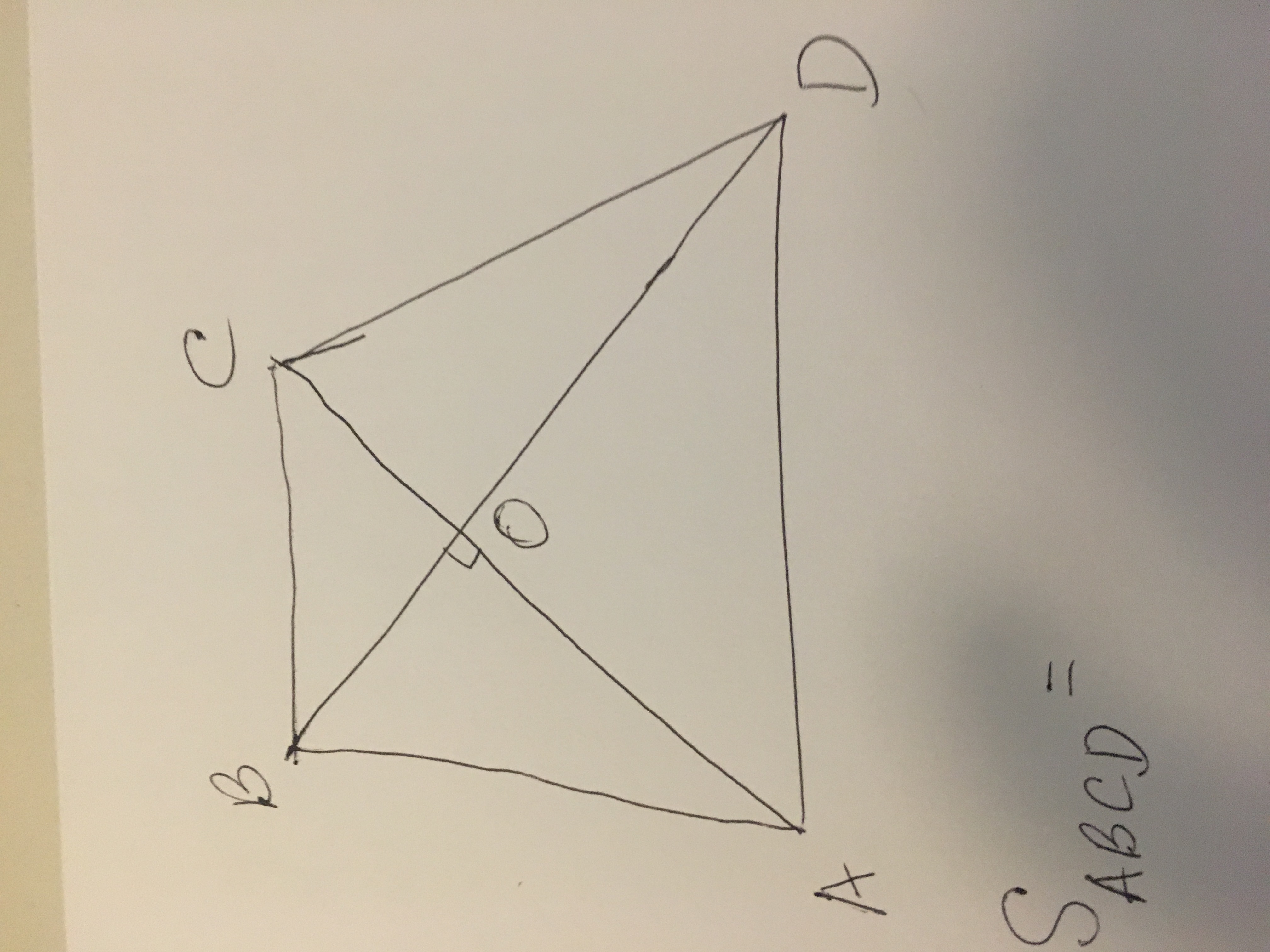
washington2:
Можно, чуть проще для 8 класса?
проще-то некуда: просто площадь четырехугольника складывается из сумм прямоугольных треуг-ков, его составляющих. А площадь каждого прямоугольного треуг-ка равна половине произведения основания на высоту..
спасибо
https://znanija.com/task/30850089 можете решить это тоже?
нее, геометрия не мой сильный конек, я больше по биологии...
Похожие вопросы
Предмет: Обществознание,
автор: amongasic
Предмет: Русский язык,
автор: Yaro367
Предмет: Биология,
автор: elvinasaripova13
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: yanikira