Question

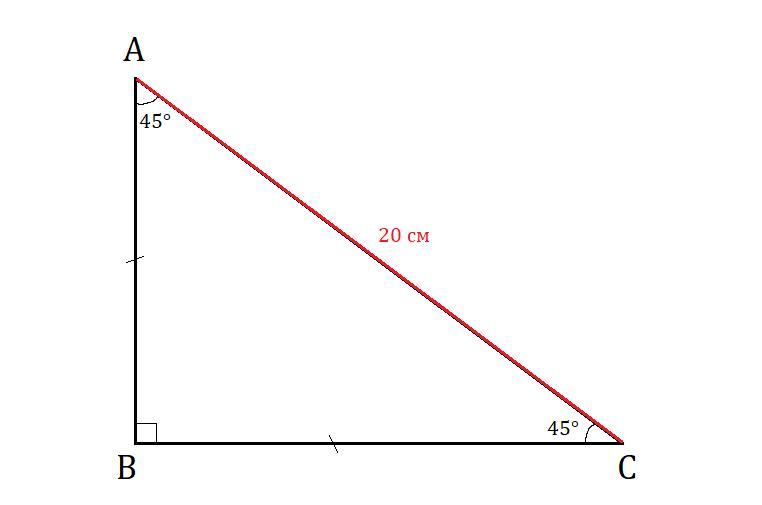
В треугольнике два угла равны 45° и 90°, а большая стороны 20 см. Найдите другие стороны треугольника.

Answer 1

Ответ:

$AB=BC= 10\sqrt{2}$ см.

Объяснение:

Пусть дан прямоугольный треугольник $ABC$ (т.к. 1 угол равен $90^{\circ}$).

Пусть $\angle B=90^{\circ}$, $\angle A=45^{\circ}$. Сторона $AC=20$ см (она же гипотенуза).

============================================================

Сумма внутренних острых углов прямоугольного тр-ка равна $90^{\circ}$.

$\Rightarrow \angle C=90^{\circ}-45^{\circ}=45^{\circ}$.

$\angle A=\angle C=45^{\circ}\Rightarrow \triangle ABC$ - равнобедренный.

$\Rightarrow AB=BC$.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Пусть $AB=BC=x$ см.

Найдём катеты $AB$ и $BC$ по теореме Пифагора $(c^2=a^2+b^2)$.

$x^2+x^2=20^2 \\ \\ 2x^2=400 \\ \\ x^2=400:2 \\ \\ x^2=200\\\\ x=\pm \sqrt{200} \\ \\ x=\pm 10\sqrt{2}$

Итак, получилось 2 корня: $x_1=10\sqrt{2}$ и $x_2=-10\sqrt{2}$. Но т.к. длина не может быть $<0$, то длина катетов равна по $10\sqrt{2}$ см.