Предмет: Геометрия,
автор: minovaksyushashai
ПОЖАЛУЙСТА ПОМОГИТЕ С ЗАДАЧЕЙ 4
Приложения:
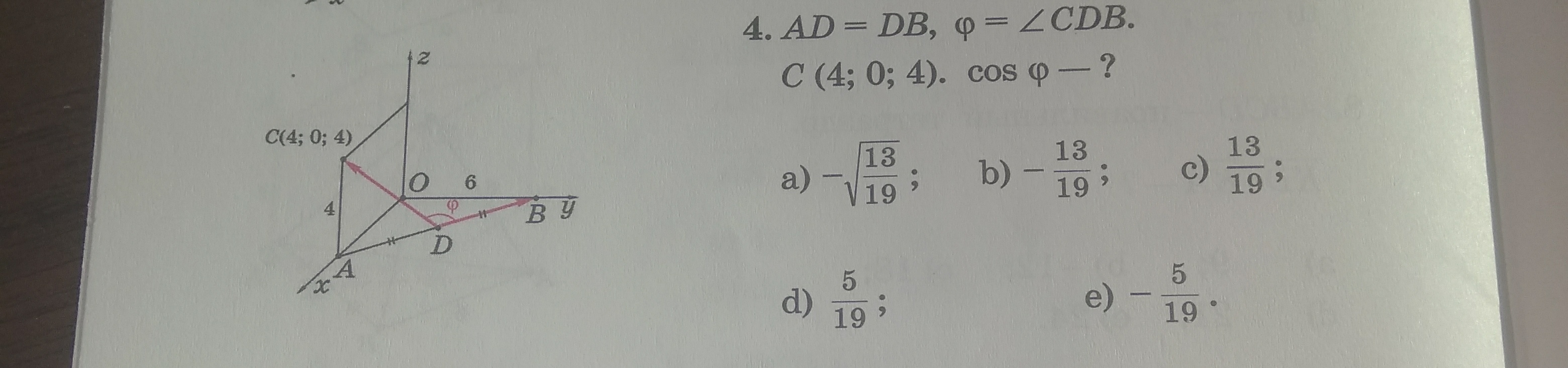
Ответы
Автор ответа:
1
4. Треугольник АОВ прямоугольный, OD - его медиана, следовательно, OD=AD=DB. ОА=4 (координата Сх точки С), Тогда координата Dx=2 (так как отрезок DDx - средняя линия треугольника АОВ). Координата Dy=3 (так как отрезок DDy - средняя линия треугольника АОВ).
Итак, координаты точек D(2;3;0), В(0;6;0) и С(4;0;4).
Тогда вектор DC{4-2;0-3;4-0} = {2;-3;4} и |DC|=√(2²+(-3)²+4²) =√29.
Вектор DB{-2;3;0} и |DB| = √(-2²+3²+0²) = √13.
Косинус угла между векторами вычисляется по формуле: cosφ=(Xa*Xb+Ya*Yb+Za*Zb)/[√(Xa²+Ya²+Xa²)*√(Xb²+Yb²+Zb²)]. Или cosφ=(-4-9+0)/√(29*13) = -√(13/29).
Ответ: Cosφ = -√(13/29). Но НИКАК не -√(13/19).
Приложения:

Аноним:
Помоги, пожалуйста с сечениями https://znanija.com/task/30824451
Похожие вопросы
Предмет: Алгебра,
автор: bamberov
Предмет: Русский язык,
автор: zr1ng
Предмет: Обществознание,
автор: ererw2q
Предмет: Математика,
автор: sova55