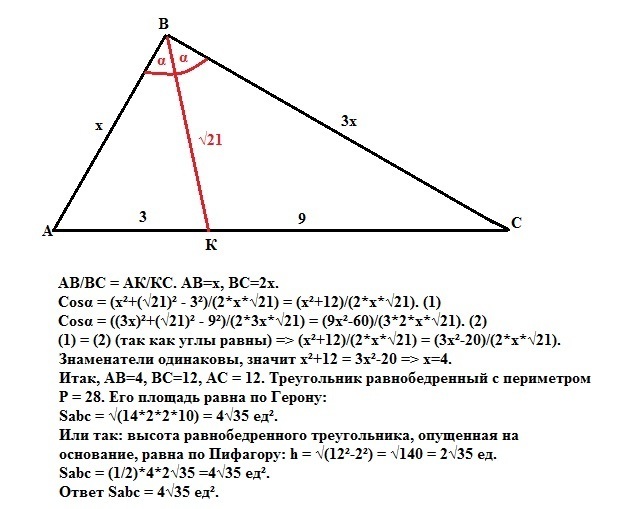
В треугольнике ABC биссектриса BK = √21,
она делит сторону AC на отрезки AK=3, KC=9 . Чему равна площадь треугольника
ABC?
Ответы
Ответ: Sabc = 4√35 ед².
Пошаговое объяснение: Биссектриса угла делит противоположную сторону в отношении прилежащих сторон. => АВ/ВС = 3/9 = 1/3.
Пусть АВ=х, тогда ВС=3х. <ABK=<CBK = α (ВК - биссектриса угла АВС). По теореме косинусов в треугольнике АВК:
Cosα = (х²+(√21)² - 3²)/(2*х*√21) = (х²+12)/(2*х*√21). (1)
По теореме косинусов в треугольнике CВК:
Cosα = ((3х)²+(√21)² - 9²)/(2*3х*√21) = (9х²-60)/(3*2*х*√21). (2)
(1) = (2) (так как углы равны) =>
(х²+12)/(2*х*√21) = (3х²-20)/(2*х*√21).
Знаменатели одинаковы, значит х²+12 = 3х²-20 => х=4.
Итак, АВ=4, ВС=12, АС = 12. Треугольник равнобедренный c периметром Р = 28. Его площадь равна по Герону:
Sabc = √(14*2*2*10) = 4√35 ед².
Или так: высота равнобедренного треугольника, опущенная на основание, равна по Пифагору:
h = √(12²-2²) = √140 = 2√35 ед.
Sabc = (1/2)*4*2√35 =4√35 ед².
Ответ Sabc = 4√35 ед².