Question

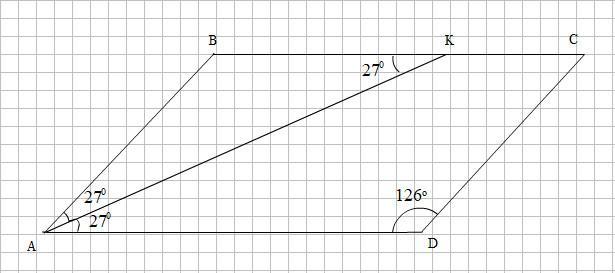
Найдите величину большего угла параллелограмма ABCD, если биссектриса угла А образует со стороной BC угол, равный 27 градусов. Ответ дайте в градусах.

Answer 1

Ответ:

Больший угол параллелограмма равен 126°

Объяснение:

Смотри рисунок в прикреплённом фото.

∠AКB = 27° (по условию)

∠DAК = ∠AКB = 27° (накрест лежащие при AD║BC и секущей АК)

∠ВАК = ∠DAК =  27°, так как АК - по условию является биссектрисой.

∠ВAD = ∠ВАК + ∠DAК  = 54°

∠ВAD  является меньшим углом параллелограмма, так как ∠ВAD < 90°.

Тогда ∠ADC - больший угол параллелограмма.

∠ADC  = 180° - ∠ВAD = 180° - 54° = 126°