Предмет: Геометрия,
автор: as19012005
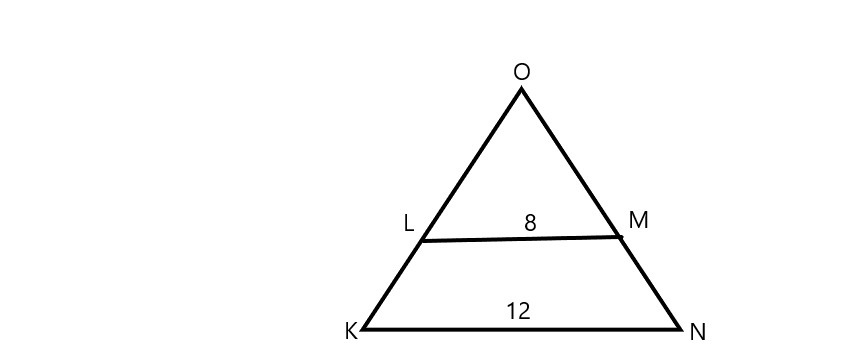
Дана равнобокая трапеция KLMN c основаниями KN=12 и LM=8. Известно, что прямые, содержащие боковые стороны трапеции, пересекаются под углом 60о. Найдите площадь трапеции.
Ответы
Автор ответа:
1
Прямые, содержащие боковые стороны равнобедренной трапеции, пересекаясь, образуют два равносторонних треугольника со сторонами 12 и 8. Площадь трапеции - разница площадей равносторонних треугольников со сторонами 12 и 8.
Площадь равностороннего треугольника - а²√3/4;
12²√3/4=36√3/4;
8²√3/4=16√3;
36√3/4-16√3=20√3 ед².
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: samsungfsamsungh
Предмет: Биология,
автор: uwuloveyou06
Предмет: Физика,
автор: t9242433533
Предмет: Алгебра,
автор: Аноним
Предмет: Алгебра,
автор: CrazyPryanik