Question

.докажите ,что уравнение  х^3-х-3=0 не имеет целых корней
.найдите корни уравнения  х^3-7х^2+7х+15=0

Answer 1

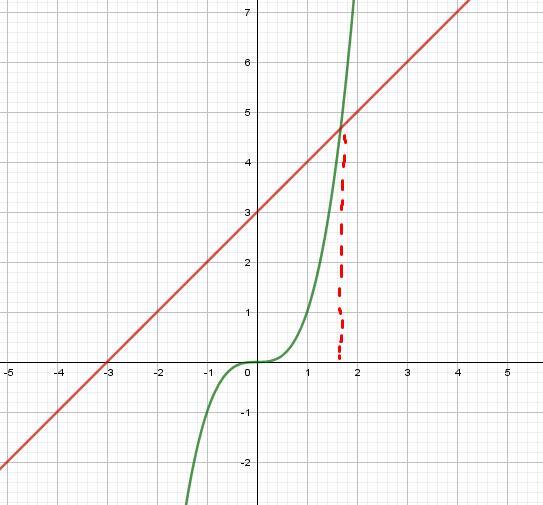
1) Построим графики функций $f(x)=x^3$ и $g(x)=3+x$ - прямую, проходящей через точки (0;3), (-3;0).

На рисунке видим, что корень уравнения принадлежит промежутку (1;2), что само собой не является целым.

2) Решим данную задачку методом разложения на множители.

$x^3-7x^2+7x+15=0\ x^3+x^2-8x^2-8x+15x+15=0\ x^2(x+1)-8x(x+1)+15(x+1)=0\ (x+1)(x^2-8x+15)=0$

Произведение двух множителей равно нулю, значит

$x+1=0~~~Rightarrow~~~ x_2=-1\ \ x^2-8x+15=0$

По т. Виета

$x_2=3;\ x_3=5$