8 класс
задание на фото
подробное решение

Ответы
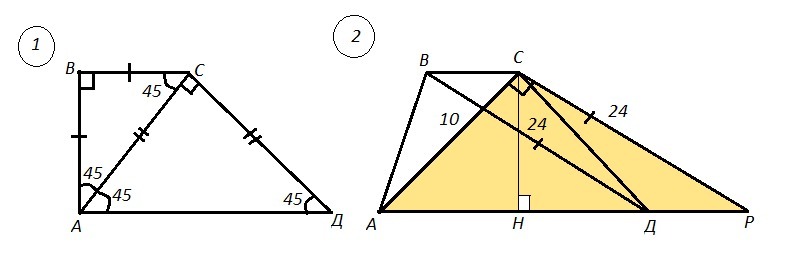
1) АВСД - трапеция, ∠ВАД=90° , АС - биссектриса ⇒ ∠ВАС=∠САД=45° , АС⊥СД ⇒ ∠АСД=90° , АС=7√3 . Найти длину средней линии трапеции m.
Рассм. ΔАСД. ∠АСД=90° , ∠САД=45° ⇒ ∠СДА=90°-∠САД=90°-45°=45° ⇒ ΔАСД - равнобедренный (при основании есть два равных угла).
АС=СД=7√2 .
АД=√(АС²+СД²)=√(АС²+АС²)=√(2АС²)=АС√2=7√2·√2=7·2=14
Рассм. ΔАВС. ∠ВАС=45°, ∠АВС=90° ⇒ ∠ВСА=90°-∠ВАС=90°-45°=45°
ΔАВС - равнобедренный (есть два равных угла) ⇒ АВ=ВС .
АС=√(АВ²+ВС²)=√(2АВ²)=АВ√2 ⇒АВ=АС:√2=7√2:√2=7 , ВС=7 .
Средняя линия трапеции равна m=(AД+BC)^2==(14+7):2=10,5 .
2) АВСД - трапеция , АС=10 см , ВД=24 см , ср.линия=m=13 см.
Найти S(АВСД).
Проведём СР║ВД , ВСРД - параллелограмм , СР=ВД=24 , РД=ВС .
Рассм. ΔАСР. АР=АД+ДР=АД+ВС ,
m=(АД+ВС)/2 , 13=(АД+ВС)/2 ⇒ (АД+ВС)=2·13=26 .
АС²+СР²=10²+24²=676 , 10²+24²=26² ⇒ ΔАСР - прямоугольный ,
∠АСР=90° .
S(АСР)=1/2·AC·CP=1/2·10·24=120
CH⊥AP : S(ACP)=1/2·AP·CH=120 , но 1/2·АР·СН=1/2·(АД+ВС)·СН=S(АВСД)
S(АВСД)=120
Площадь трапеции АВСД равна площади треугольника АСР.