Предмет: Геометрия,
автор: ан123321
98б!!!!!!!!!!!!!!!!
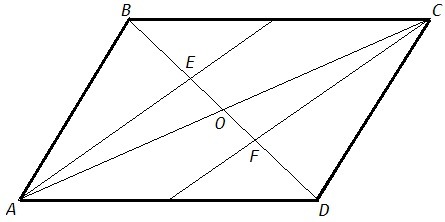
Дан параллелограмм ABCD. Докажите, что точки пересечения медиан треугольников ABC и CDA лежат на диагонали BD и делят ее на 3 равные части.
Ответы
Автор ответа:
1
Диагонали параллелограмма точкой пересечения делятся пополам.
О - точка пересечения диагоналей, AO=CO, BO=DO=1/2 BD
BO - медиана в △ABC, DO - медиана в △CDA.
Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
E - точка пересечения медиан в △ABC,
BE=2/3 BO =1/3 BD, EO=1/3 BO =1/6 BD
F - точка пересечения медиан в △CDA,
DF=2/3 DO =1/3 BD, FO=1/3 DO =1/6 BD
EF= EO+FO =2/6 BD =1/3 BD
Приложения:
Похожие вопросы
Предмет: История,
автор: amirka5833
Предмет: Алгебра,
автор: leno4kaf0r3v3r
Предмет: Геометрия,
автор: utubp074
Предмет: Математика,
автор: ника685
Предмет: Математика,
автор: Аноним