СРОЧНО нужно 1 и 2!!! Завтра зачет!!! Помогите пожалуйста!!!

Ответы
1.
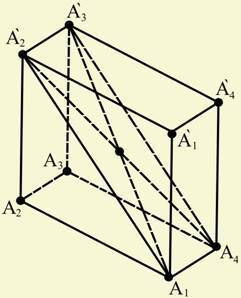
Доказательство. Рассмотрим какие-либо две диагонали параллелепипеда, например и (рис. 18). Так как четырехугольники и - параллелограммы с общей стороной, то их стороны и параллельные друг другу, а значит, лежат в одной плоскости. Эта плоскость пересекает плоскости противоположных граней параллелепипеда по параллельным прямым и. Итак, четырехугольник - параллелограмм. Диагонали параллелепипеда и является диагоналями этого параллелограмма. Поэтому они пересекаются и точкой пересечения O делятся пополам.
Аналогично доказывается, что диагонали и, а также диагонали и пересекаются и точкой пересечения делятся пополам. Отсюда заключаем, что все четыре диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам. Теорема доказана.
Из теоремы 1.3 следует, что точка пересечения диагоналей параллелепипеда является его центром симметрии.