Предмет: Алгебра,
автор: CrazyD0C
Упростите,пожалуйста
Приложения:
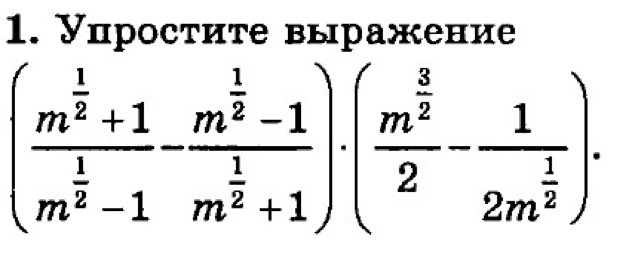
Ответы
Автор ответа:
0
Приложения:

CrazyD0C:
Отлично,пойду за декодером
Уже не надо,в интернете нашёл
Зачем что-то искать? Вы не видите нормальное решение?
Один текст
Подождите, добавлю скрин
Ладно уже,я в интернете нашёл,зато баллы потерял(
CrazyD0C, так видно?
Если можете,то на другой вопрос ответьте,там система уравнений,в профиле найдёте,я думаю
Возможно это из-за того,что я с телефона
Похожие вопросы