Question

95 баллов. Помогите решить 2 и 4 номер.

Answer 1

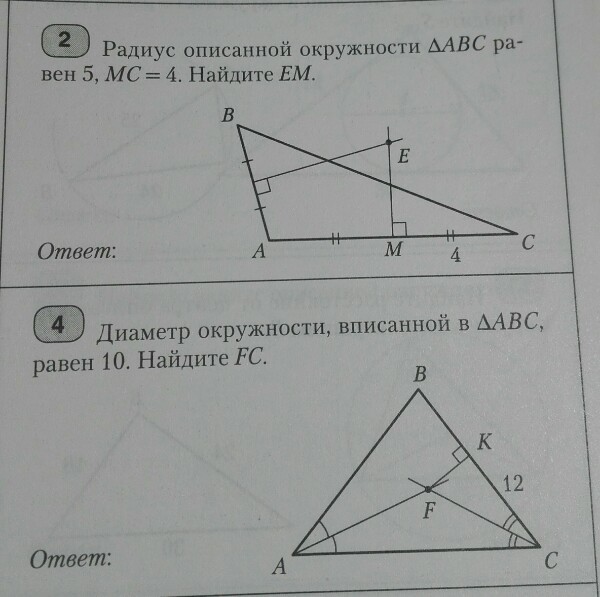
2. Точка Е пересечения серединных перпендикуляров, проведенных к сторонам треугольника (см. рисунок), является центром окружности, описанной около этого треугольника. Следовательно отрезки АЕ=ВЕ=СЕ=5.

Соединим точки А и Е. АМ=МС = 4 (дано). Тогда по Пифагору из треугольника АЕМ  ЕМ = √(5²-4²) = 3 ед.

4. Точка F пересечения биссектрис внутренних углов треугольника треугольника (см. рисунок) является центром окружности, вписанной в этот треугольник. Значит отрезок FK = равен 10:2 = 5. И если СК =12 (по рисунку), то по Пифагору их треугольника FKC

FC = √(12²+5²) = 13 ед.

Answer 2

2) Центром описанной окружности около треугольника является точка пересечения серединных перпендикуляров. Центр описанной окружности равноудалён от вершин данного треугольника. Следовательно, АЕ = ВЕ = СЕ = 5 - радиус описанной окружности.
Рассмотрим тр. ЕМС: по т. Пифагора
ЕМ = V( 5^2 - 4^2 ) = V( 25 - 16 ) = V9 = 3

ОТВЕТ: 3

3) Центром вписанной окружности в треугольник является точка пересечения биссектрис. Центр вписанной окружности равноудалён от сторон данного треугольника. Следовательно, FK = 10/2 = 5 - радиус вписанной окружности.
Рассмотрим тр. FKC: по т. Пифагора
FC = V( 5^2 + 12^2 ) = V( 25 + 144 ) = V169 = 13

ОТВЕТ: 13.