Предмет: Алгебра,
автор: nujomi
Всем привет, помогите пожалуйста найти определенный интеграл функции:
Приложения:
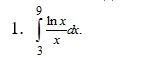
Ответы
Автор ответа:
2
nujomi:
Спасибо огромное!
Автор ответа:
1
Похожие вопросы
Предмет: География,
автор: sakura9413
Предмет: Математика,
автор: bablkvaser228
Предмет: История,
автор: nurdauletbazarbekov0
Предмет: География,
автор: Аноним
Предмет: Обществознание,
автор: galinamysak1963