Предмет: Алгебра,
автор: Кариночка78
Составьте уравнение касательной и нормали к кривой в точке, соответствующей значению параметра t=t0
Приложения:
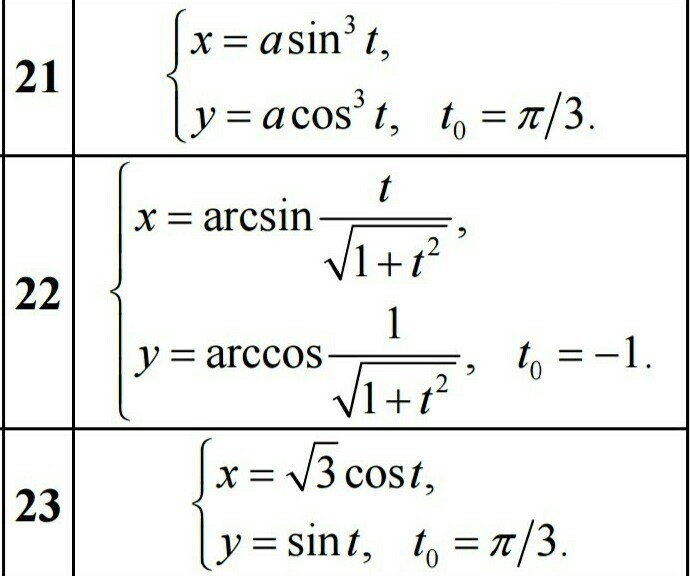
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Литература,
автор: okaevislam80
Предмет: Математика,
автор: rqh7p4mkwy
Предмет: Русский язык,
автор: ninsanofa
Предмет: Математика,
автор: Саида1111
Предмет: Математика,
автор: varvara3333