Question

Помогите ответить с решением, пожалуйста.

Окружность, построенная как на диаметре на стороне AD параллелограмма ABCD, проходит через точку пересечения диагоналей параллелограмма и пересекает сторону AB в её середине. Найти диагонали параллелограмма, если периметр параллелограмма равен 32.

Answer 1

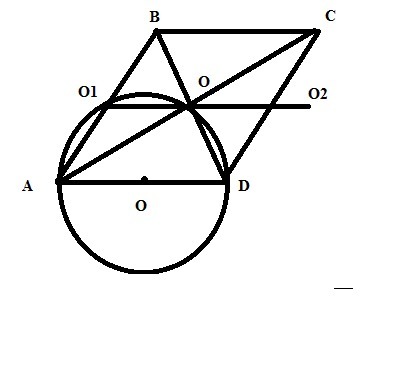
О1-середина АВ, О-середина BD, значит ОО1-средняя линия ΔABD , AO1OD-трапеция и OO1=AD/2=R

Соединив О1  и О с О2-получим 3 равносторонних треугольника со стороной R, значит AO1OD-равнобедренная трапеция, <O1AD=<ADO=60; AO1=O1O=OD=R=AD/2

Тогда AB=2AO1=2R, значит AD=AB-и ABCD-ромб со стороной , равной P/4=32/4=8; R=AD/2=4

Осталось найти диагонали ромба. ОD=R; BD=2OD=2*4=8

Рассмотрю ΔAOD-прямоугольный т к диагонали ромба перпендикулярны

AO^2=AD^2-OD^2=8^2-4^2=64-16=48; AO=4 корня из 3

Тогда диагональ АС=2АО=8 корней из 3

Ответ диагонали 8 и 8 корней из 3