Предмет: Алгебра,
автор: милославаru
Решите логарифмическое неравенство (x^2-4)* log1/2 (x^2+1)
Приложения:
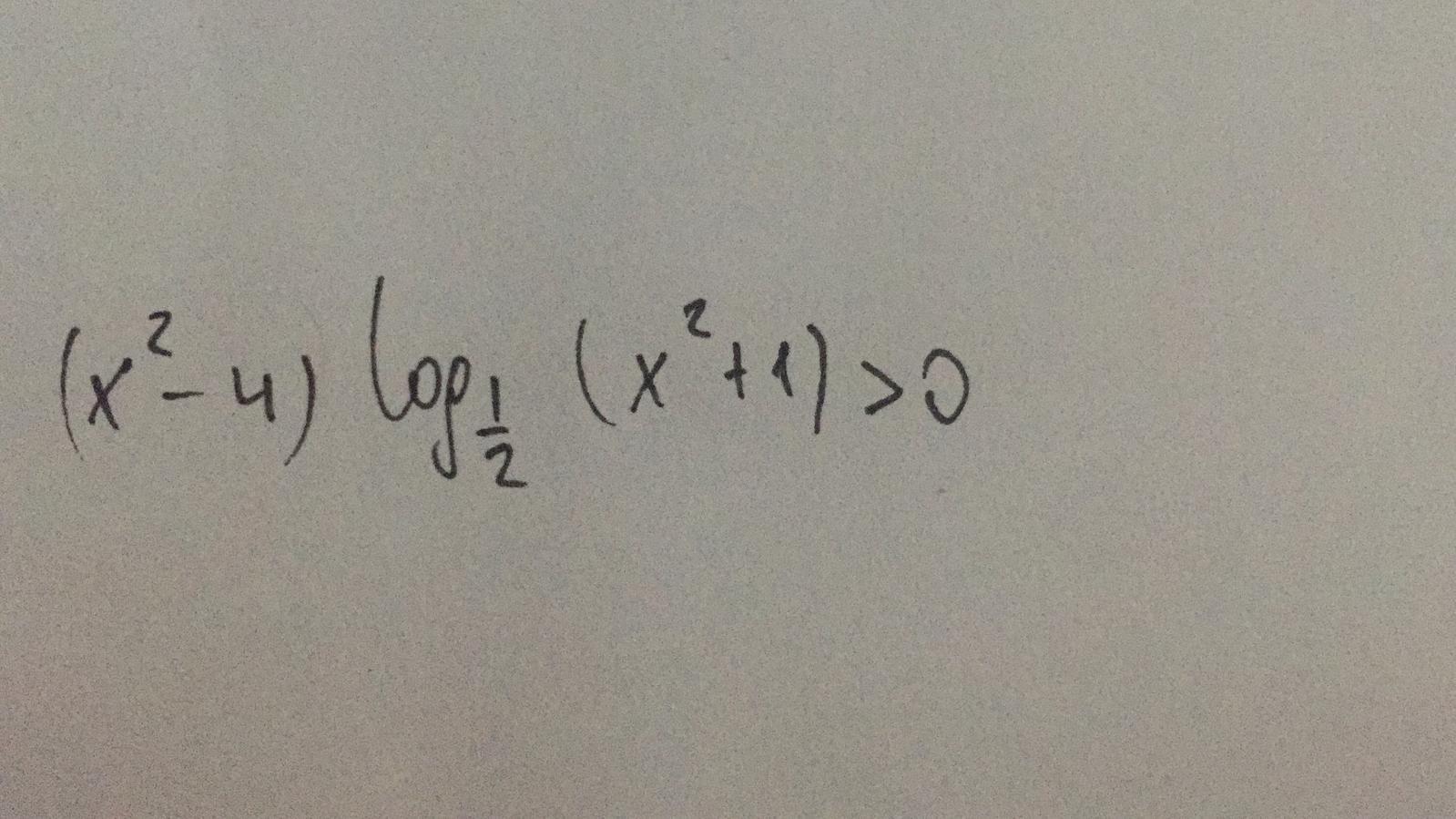
Ответы
Автор ответа:
3
Автор ответа:
1
task/30688676 Решите логарифмическое неравенство
(x²- 4) log_(1/2) (x²+1) > 0
решение x²+ 1 ≥ 1 равенство выполняется при x = 0 , что, очевидно, не явлется решением неравенства [ log_(1/2) 1 = 0 ] .
(x²- 4) log_(1/2) (x²+1) > 0 ⇔ { x²- 4 < 0 ; x ≠ 0. ⇔ { (x +2)*(x - 2) < 0 ; x ≠ 0. ⇔ { x ∈( -2 ; 2) ; x ≠ 0. ⇔ x ∈ ( -2 ;0 ) ∪ (0 ;2) .
ответ : x ∈ ( -2 ;0 ) ∪ (0 ;2)
* * * x ≠ 0 log_(1/2) (x²+1) < log_(1/2) 1 < 0 ; 0 < осн.лог.=1/2 < 1 * * *
Похожие вопросы
Предмет: Математика,
автор: gajdarovalaura9
Предмет: Английский язык,
автор: Geh28b3veuwu
Предмет: Математика,
автор: abdiaika84
Предмет: Литература,
автор: slavikkuzmenko