Question

Помогите пожалуйста с Геометрией!
Биссектриса угла C параллелограмма ABCDпересекает сторону AB в точке F, а продолжение стороны AD в точке K. Известно, что BF=5 и AK=4. Найти стороны параллелограмма.

Answer 1

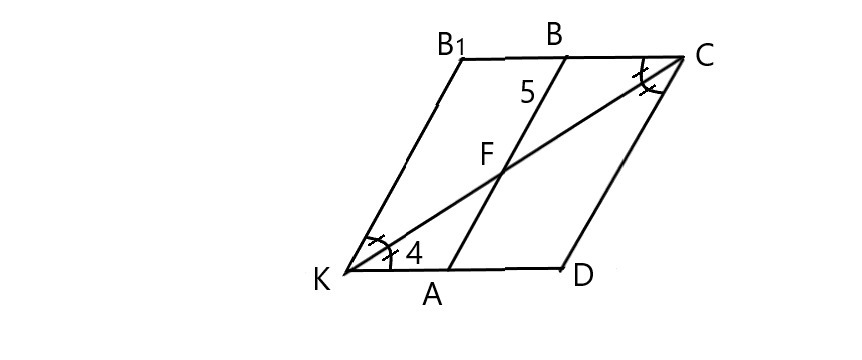
Биссектриса, проведенная из вершины параллелограмма, отсекает равнобедренный треугольник. Значит BF=BC=5.

Достроим - КВ₁ параллельно СD и продолжение ВС.

KB₁BA - параллелограмм, КС - биссектриса угла К, значит АК=АF=4. Значит АВ=AF+FB=4+5=9.

Answer 2

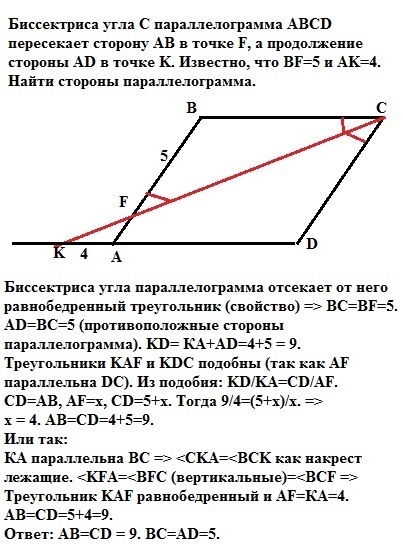
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник (свойство) => ВС=ВF=5.

AD=BC=5 (противоположные стороны параллелограмма). KD= КА+AD=4+5 = 9.

Треугольники KAF и KDC подобны (так как AF параллельна DC). Из подобия: KD/KA=CD/AF.

CD=AB, AF=x, CD=5+x. Тогда 9/4=(5+x)/x. =>

х = 4. АВ=CD=4+5=9.

Или так:

КА параллельна ВС => <CKA=<BCK как накрест лежащие. <KFA=<BFC (вертикальные)=<BCF =>

Треугольник KAF равнобедренный и AF=КА=4.

АВ=CD=5+4=9.

Ответ: АВ=CD = 9. BC=AD=5.