Предмет: Алгебра,
автор: bondarenkonekita
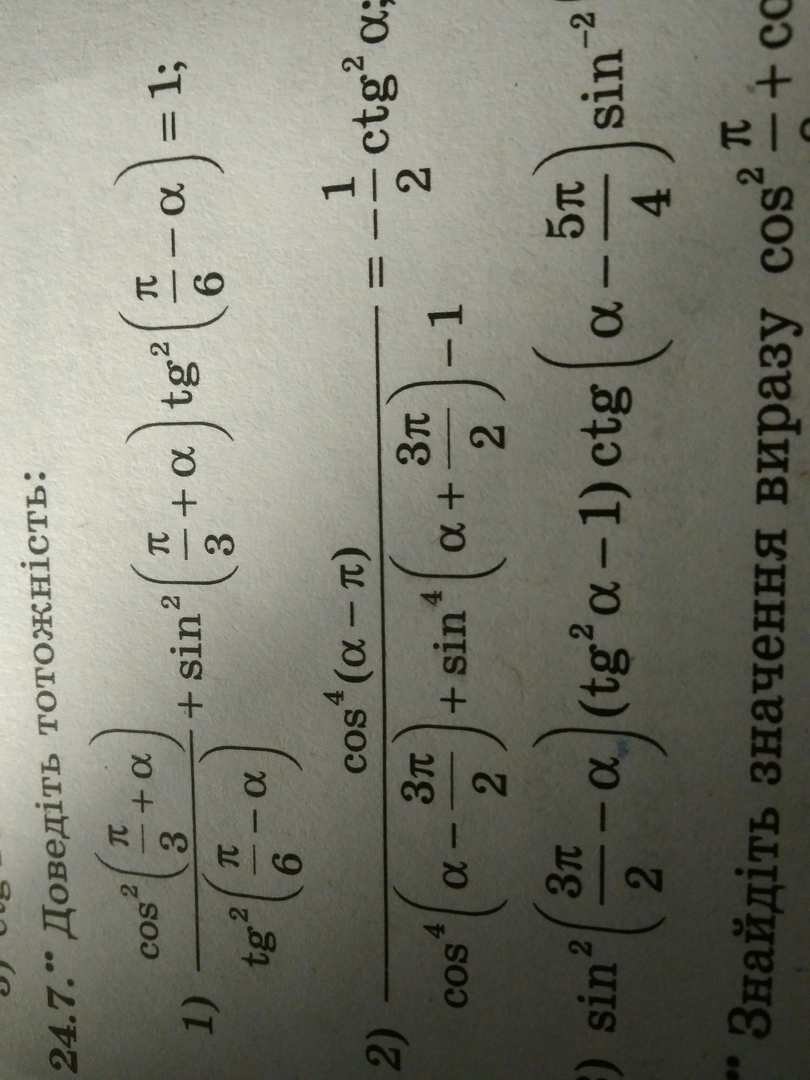
14 БАЛЛОВ ! Решите пж первый пример
Приложения:
Ответы
Автор ответа:
1
Для удобства записи обозначим углы
Похожие вопросы
Предмет: Английский язык,
автор: tam89589
Предмет: Математика,
автор: Аноним
Предмет: География,
автор: nadja220376
Предмет: Математика,
автор: vaflek33