Предмет: Математика,
автор: BABYSTORM
СРОЧНО,РЕШИТЕЕ
Там решение в некоторых должно быть связано с теоремой минусов и косинусов
Приложения:
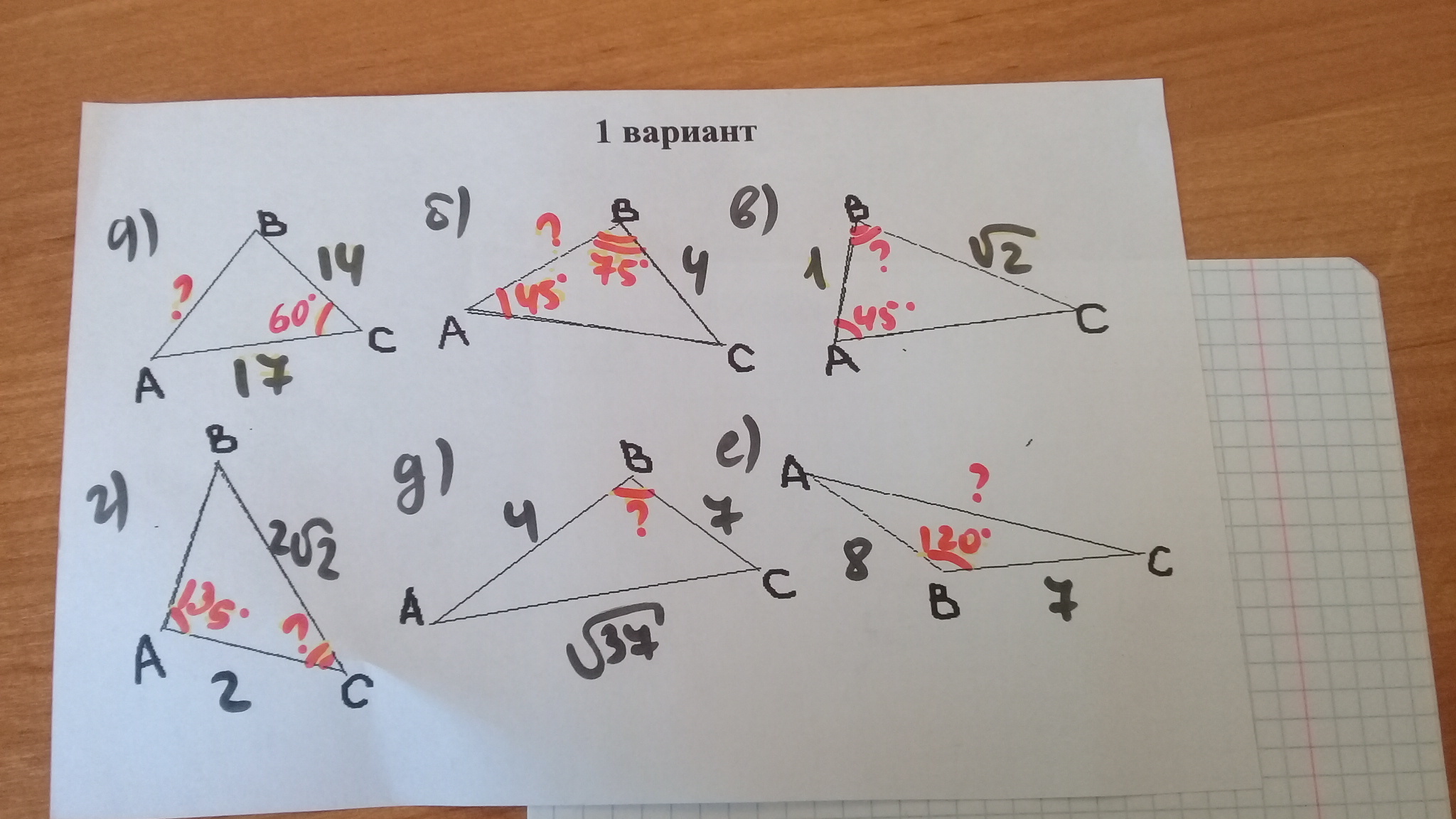
Ответы
Автор ответа:
1
а) AB² = 14² + 17² -2*14*17*cos60° = 196 + 289 - 238 = 247
AB = √247
б) ∠C = 180° - 45° - 75° = 60°
AB/sin60° = BC/sin45° = 2√2
AB = 2√2*√3/2 = √6
в) BC/sin45° = AB/sinC
sinC = √2/2 : √2 = 1/2
∠C = 30°
∠B = 180° - 45° - 30° = 105°
г) AC/sinB = BC/sin135°
sinB = 2*√2/2 : 2√2 = 1/2
∠B = 30°
∠C = 180° - 135° - 30° = 15°
д) cosB = (4² + 7² - (√37)²) : (2*4*7) = (16 + 49 - 37) : 56 = 28 : 56 = 1/2
∠B = 60°
е) AC² = 8² + 7² - 2*8*7*cos120° = 64 + 49 + 56 = 169
AC = 13
Автор ответа:
1
Ответ:
Пошаговое объяснение:
a) По теореме косинусов:
б) ∠BCA=180°-∠CAB-∠CBA=60
По теореме синусов:
в) По теореме синусов
∠BCA=30°
∠CBA=180°-30°-45°=115°
г) По теореме синусов
∠ABC=30°
∠ACB=180°-30°-135°=15°
д) По теореме косинусов:
∠ABC=60°
е) По теореме косинусов
AC=13
Похожие вопросы
Предмет: Українська мова,
автор: petrovicfeda97
Предмет: Алгебра,
автор: tanya0047169
Предмет: Химия,
автор: t0al0ne
Предмет: Математика,
автор: KareyevaD