Question

Даю70баллов, хэлп!!!

Обьясните, пожалуйста, кто нибудь, как решать такие задачи!!?

Answer 1

Подобные задачи удобно решать, перейдя от малопонятной начинающим алгебры логики к самой обычной алгебре. Нужно тольео немного "подправить" привычные алгебраические законы.

Значение "Ложно" - это 0. Значение "Истинно" - это не ноль. Например, 1.

Тогда нужно подправить лишь одно правило: 1 + х = 1. Действительно, такая сумма всегда не меньше 1, т.е. она не 0, значит, она 1.

В обычной алгебре нет операций ∧, ∨,  отрицания (надчеркивание), и импликации (→). Операцию ∧ ("И") мы будем заменять умножением, операцию ∨ ("ИЛИ") - сложением, отрицание (инверсия) - это замена 1 на 0 и 0 на 1. Импликацию заменим равносильным преобразованием.

Пример а)

$(Д\L\to M)\land N=(\overline L+M)\cdot N$

Когда произведение равно 1? Когда оба сомножителя равны 1. Следовательно, N=1 и сумма в скобках также равна 1. Это возможно при M=1 и любом L или при L=0 (отрицание 0 даст 1) и любом М.

Получаем  тройки (L,M,N) = (0,0,1), (0,1,1), (1,1,1).

Пример б)

$L((L\to M)\to (L\land N))=L((\overline L+M)\to LN)=L(\overline{\overline L+M}+LN)=\\L(L\overline M+LN)=LL(\overline M+N)=L(\overline M+N)$

Полученное выражение анализируется аналогично предыдущему примеру. Получаем тройки (L,M,N) = (1,0,0), (1,0,1),(1,1,1).

Пример в)

$(L\lor M)\to(\overline L\land N)=(L+M)\to \overline LN=\overline{L+M}+\overline LN=\\\overline L\cdot \overline M+\overline LN=\overline L(\overline M+N)$

И снова полученное выражение аналогично предыдущим примерам дает три тройки: (L,M,N) = (0,0,0), (0,0,1), (0,1,1)

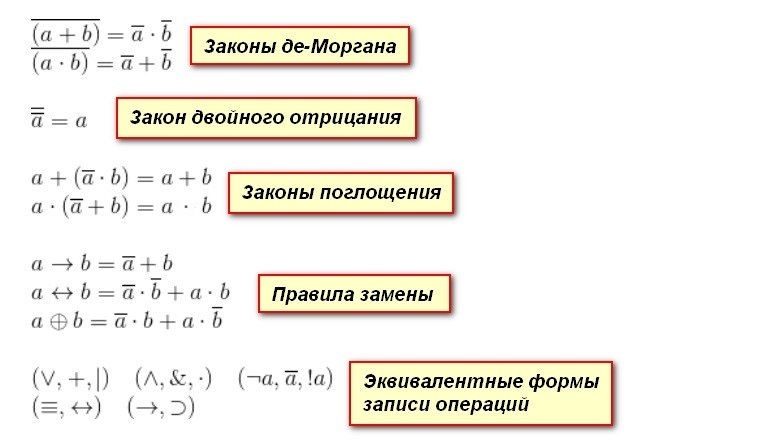
Во вложении есть дополнительная информация, которая может помочь понять тему.