Предмет: Математика,
автор: luhan1658
Комбинаторика.
Решить уравнение: под цифрой 9
Приложения:
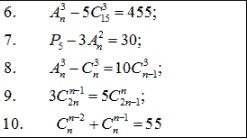
Ответы
Автор ответа:
1
Ответ: n=5
Пошаговое объяснение:
Перенесём дроби в одну часть (левую) и вынесем общий множитель.
Т.к. факториал принимает значения от 1 до плюс бесконечности, то равенство может обратиться в ноль только благодаря разности в скобке.
Сделаем проверку:
Похожие вопросы
Предмет: Математика,
автор: Kurnasay
Предмет: Физика,
автор: elenaelcova413
Предмет: Математика,
автор: vfertiluk
Предмет: Химия,
автор: nastay20002
Предмет: Литература,
автор: millamalinina