Предмет: Алгебра,
автор: 1234567011
СРОЧНО 35 БАЛЛОВ Найти неопределенные интегралы. Результаты проверить дифференцированием. Сделайте хотя бы два пожалуйста. Заранее спасибо)
Приложения:
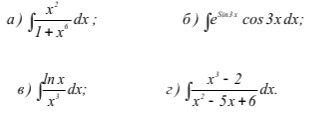
Ответы
Автор ответа:
0
Решаем методом внесения под знак дифференциала
а)
б)
Похожие вопросы
Предмет: Математика,
автор: poplavskiyandrey80
Предмет: Литература,
автор: darakonosenko40
Предмет: Английский язык,
автор: tamoe718
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: bosskm2000