Question

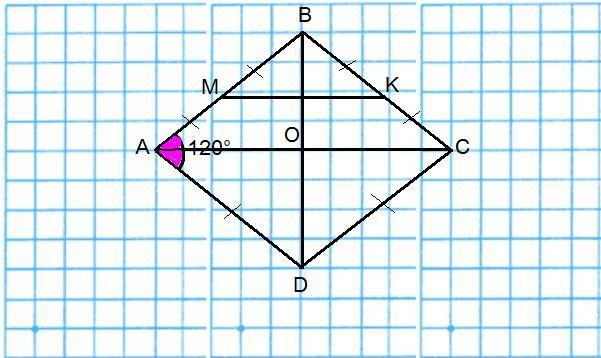
периметр ромба ABCD равен 48 см. Угол A=120 градусов. Найдите среднюю линию МК треугольника АВС, где М принадлежит АВ, К принадлежит ВС.


Полное решение пожалуйста, со всеми объяснениями.

Answer 1

Ответ: 6 см.

Пошаговое объяснение:

Ромб - параллелограмм, у которого все стороны равны.

⇒ АВ = ВС = CD = AD = P/4, где Р - периметр ромба ABCD.

АВ = ВС = CD = AD = 48/4 = 12 см.

Проведём в ромбе ABCD  диагонали BD и AC.

Диагонали ромба взаимно перпендикулярны делят его углы пополам.

⇒ ∠ВАО = 120°/2 = 60°

ΔВАО - прямоугольный, так как диагонали ромба взаимно перпендикулярны.

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠АВО = 90° - ∠ВАО = 90° - 60° = 30° ⇒ ∠АВС = ∠АВО * 2 = 30° * 2 = 60°(диагонали ромба делят его углы пополам)

Сумма внутренних углов треугольника равна 180°.

⇒ ∠ВСО = 180° - (60° + 60°) = 180° - 120° = 60°

⇒ ΔАВС - равносторонний, так как все его углы равны по 60°.

⇒ АВ = ВС = АС = 12 см.

Средняя линия треугольника равна половине длины основания этого треугольника.

⇒ МК = 12/2 = 6 см.