Question

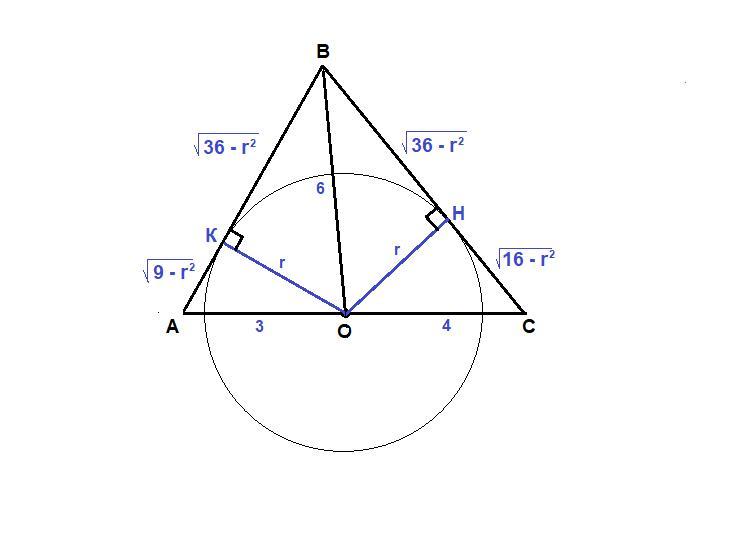
Окружность с центром О на стороне АС треугольника АВС касается сторон АВ и ВС. Известно, что AO = 3, OC = 4 и BO = 6. Найти радиус окружности и площадь треугольника АВС. Прошу подробное решение.

Answer 1

Ответ:     r = 3√15/4      

                S = 63√15 / 8

Объяснение:

ОК⊥АВ и ОН⊥ВС как радиусы, проведенные в точки касания.

ОК = ОН = r,

ОВ - общая сторона для треугольников ВОК и ВОН, ⇒

ΔВОК = ΔВОН по катету и гипотенузе, ⇒

∠ОВК = ∠ОВН, ⇒

ВО - биссектриса угла АВС.

Из прямоугольных треугольников по теореме Пифагора выразим отрезки сторон АВ и ВС:

AK = √(9 - r²)

KB = √(36 - r²)

BH = √(36 - r²)

HC = √(16 - r²), тогда

АВ = √(9 - r²) + √(36 - r²)

ВС = √(16 - r²) + √(36 - r²)

По свойству биссектрисы угла треугольника:

АВ : ВС = АО : ОС

$\frac{\sqrt{9-r^{2}}+\sqrt{36-r^{2}}}{\sqrt{36-r^{2}}+\sqrt{16-r^{2}}}=\frac{3}{4}$

$4\sqrt{9-r^{2}}+4\sqrt{36-r^{2}}=3\sqrt{36-r^{2}}+3\sqrt{16-r^{2}}$

$4\sqrt{9-r^{2}}+\sqrt{36-r^{2}}=3\sqrt{16-r^{2}}$

Возводим обе части уравнения в квадрат:

16(9 - r²) + 8√(36 - r²)√(9 - r²) + 36 - r² = 9(16 - r²)

144 - 16r² + 8√(36 - r²)√(9 - r²) + 36 - r² = 144 - 9r²

8√(36 - r²)√(9 - r²) = 8r² - 36

2√(36 - r²)√(9 - r²) = 2r² - 9

Возводим в квадрат еще раз:

4(36 - r²) · (9 - r²) = 4r⁴ - 36r² + 81

4(324 - 45r² + r⁴) = 4r⁴ - 36r² + 81

1296 - 180r² + 4r⁴ = 4r⁴ - 36r² + 81

144r² = 1215

r² = 135/16

r = 3√15/4

AB = √(9 - 135/16) + √(36 - 135/16) = √((144 - 135) / 16) + √((576 - 135) / 16) =

= √(9/16) + √(441/16) = 3/4 + 21/4 = 24/4 = 6

BC = √(36 - 135/16) + √(16 - 135/16) = 21/4 + √((256 - 135) / 16) =

=21/4 + √(121/16) = 21/4 + 11/4 = 32/4 = 8

Полупериметр:

p = (AB + BC + AC)/2 = (6 + 8 + 7)/2 = 21/2

S = pr

S = 21/2 · 3√15/4 = 63√15/8 кв. ед.