Предмет: Алгебра,
автор: fedotka111
Мужики в кротчайшие сроки надо
Приложения:

Ответы
Автор ответа:
2
Автор ответа:
2
Решение во вложении...
Приложения:
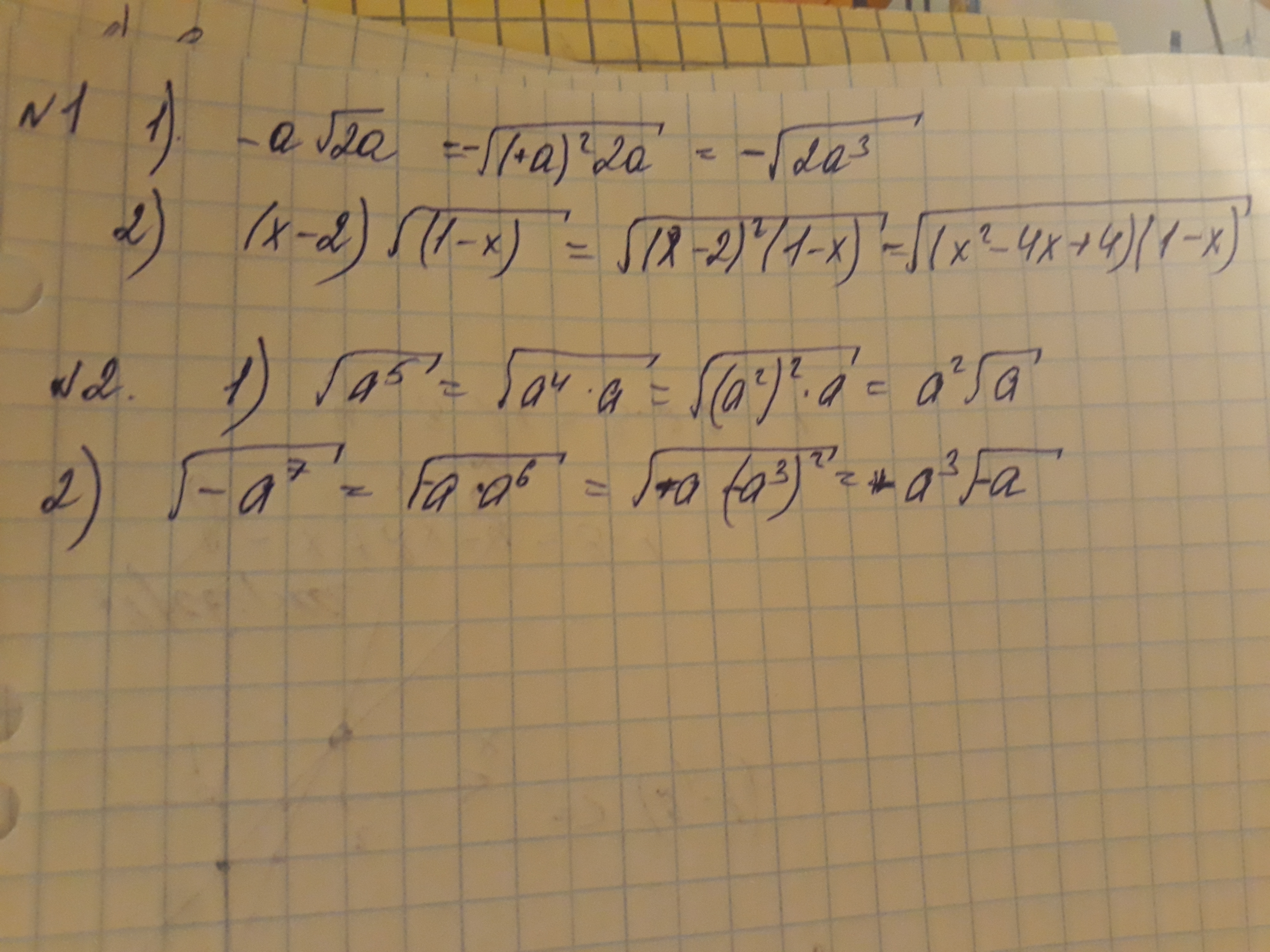
Похожие вопросы
Предмет: Информатика,
автор: Аноним
Предмет: Английский язык,
автор: vika154344
Предмет: Информатика,
автор: glazevmisha
Предмет: Алгебра,
автор: dimakaminsky2
Предмет: Химия,
автор: iskakovastam1