НА ПОМОЩЬ !!!
Из вершины C прямоугольного треугольника abc(c=90) проведен перпендикуляр CD к его плоскостям. Найти длинy наклонных AD и BD а так же длину перпендикуляра CD при следующих длинах:
Угол CAB 30°
Угол ADC 45°
AC 20
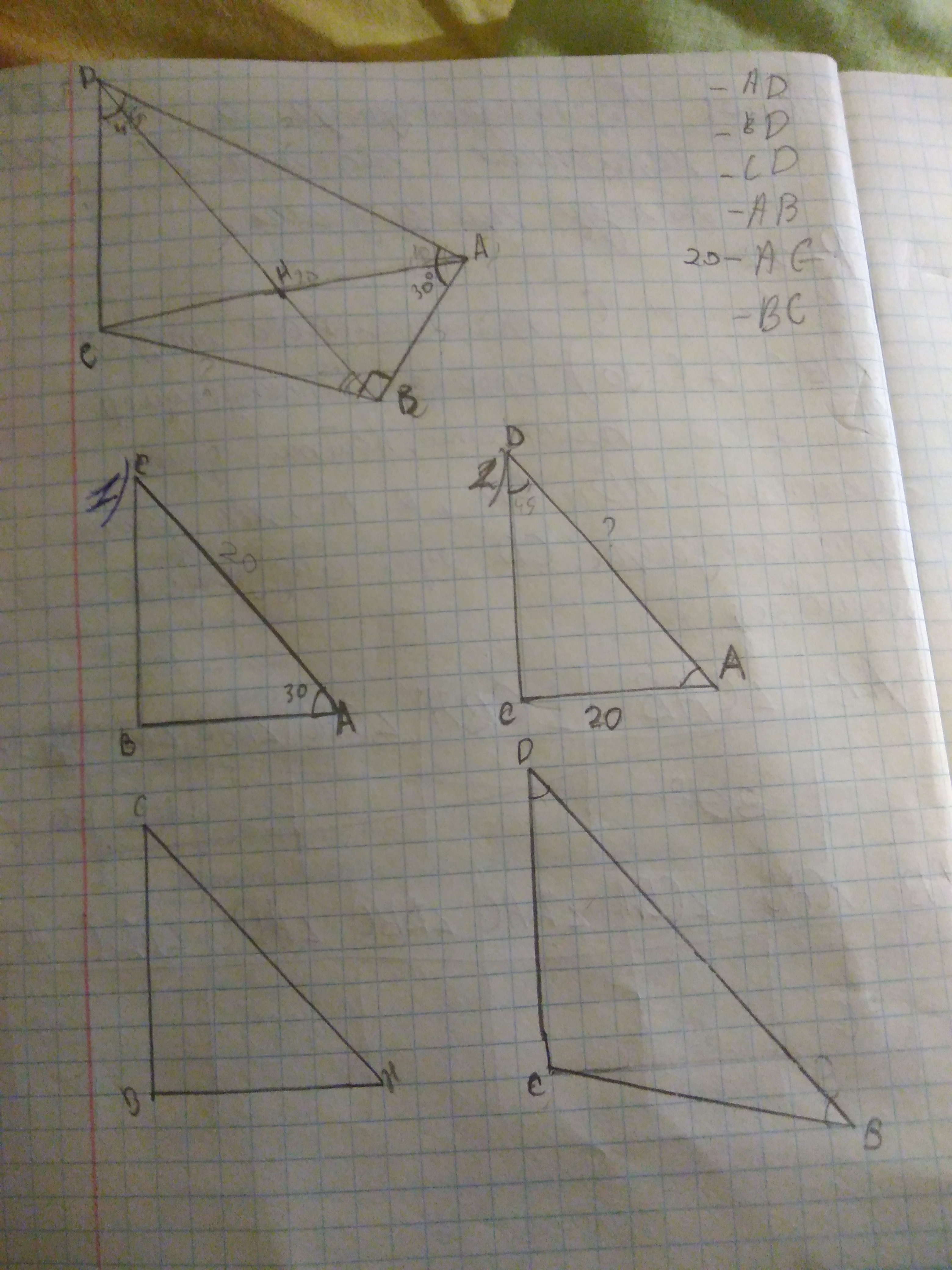
Ответы
Ответ:
Пошаговое объяснение:

task/30605008
Дано ΔABC : ∠ACB =90° ; CD⊥ (ABC) ; ∠CAB =30° ; ∠ADC =45° ; AC =20 . -----------
AD -? , BD - ? CD - ?
решение : Треугольники ACD и ВCD прямоугольные , т.к. DC ⊥ (ABC) ⇒ DC ⊥ CA и DC ⊥ СВ .
Из ΔACD: ∠ADC =45° ⇒ ∠DAC =90° - ∠ADC =90° - 45°= 45° , поэтому прямоугольный треугольник ACD еще и равнобедренный CD = CA =20 . AD =√(CA²+CD²) = √(CA²+CA²) =√(2CA²) =CA√2 = 20√2 .
В ΔABC : CB = AB/2 (как катет против угла 30°) ⇒ AB =2СВ ; по теореме Пифагора: AC=√(AB² - CB²) = √( (2CB)² - CB²) = √( 4CB² - CB²) =√(3CB²) = CB√3 ⇒ CB = AC/√3 =20 /√3 || AB =2CB =40/√3 ||
Из ΔBCD: BD =√(BC²+DC²) =√( (20/√3)²+20²) =√( 20²(1/3+1 )=√( 20²*4/3 ) = 20*2 /√3 = 40 /√3 =(40√3) /3 .
Ответ: AD = 20√2 ; BD =(40√3) /3 ; CD =20 .
P.S. ! ΔCDB = ΔCAB ( CA _общий катет и CD=AC ⇒ BD=AB )