Question

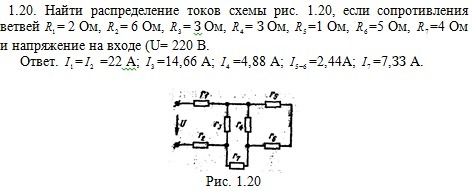
Помогите пожалуйста решить задачу

Answer 1

1. Заменим последовательные сопротивления  $R_5$ и $R_6$ на $R_{56}$:

$R_{56} = R_5 + R_6 = 6 \Omega$

2. Сопротивления $R_4$ и $R_{56}$ расположены  параллельно, заменим их на $R_{456}$:

$R_{456} = \frac{R_4 \cdot R_{56}}{R_{4} + R_{56}} = 2 \Omega$

3. Заменим последовательные сопротивления  $R_7$ и $R_{456}$ на $R_{4567}$:

$R_{4567} = R_7 + R_{456} = 6 \Omega$

4. Сопротивления $R_3$ и $R_{4567}$ расположены  параллельно, заменим их на $R_{34567}$:

$R_{34567} = \frac{R_3 \cdot R_{4567}}{R_{3} + R_{4567}} = 2 \Omega$

5. Сопротивления  $R_1$,  $R_2$ и $R_{34567}$ расположены последовательно, поэтому эквивалентной сопротивление схемы равно:

$R = R_1 + R_2 + R_{34567} = 10 \Omega$

6. В последовательно расположенных сопротивлениях ток одинаков:

$I_1 = I_2 = \frac{U}{R} = \frac{220B}{10 \Omega} = 22A$

7. Падение напряжения на $R_{34567}$ (а, следовательно и на параллельно расположенных  $R_{3}$ и $R_{4567}$) составляет:

$U_3 = \frac{R_{34567}}{R} \cdot U = \frac{2 \cdot 220}{10} = 44B$

Тогда $I_3 = \frac{U_3}{R_3} = \frac{44B}{3\Omega} = 14,66A$

8. Через последовательно расположенные $R_{7}$ и $R_{456}$ идет ток: $I_7 = \frac{U_3}{R_{4567}}=\frac{44B}{6\Omega} = 7,33A$

9. Падение напряжения на $R_{456}$ (а, следовательно и на параллельно расположенных  $R_{4}$ и $R_{56}$) составляет:

$U_4 = U_3 \cdot \frac{R_{456}}{R_{4567}}= 44B \cdot \frac{2}{6}=14,66B$

Находим ток через $R_{4}$:

$I_4 =\frac{U_4}{R_4} = \frac{14,66B}{3 \Omega} = 4,88A$

10. В последовательно расположенных $R_{5}$ и $R_{6}$ ток одинаков и равен:

$I_5 = I_6 = \frac{U_4}{R_{56}}=\frac{14,66B}{6\Omega} = 2,44A$