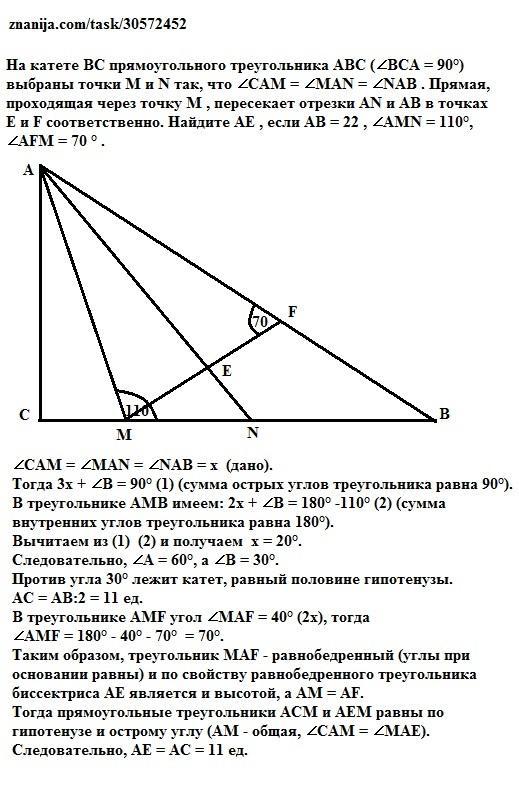
На катете B C прямоугольного треугольника A B C ( ∠ B C A = 90 ° ) выбраны точки M и N так, что ∠ C A M = ∠ M A N = ∠ N A B . Прямая, проходящая через точку M , пересекает отрезки A N и A B в точках E и F соответственно. Найдите A E , если A B = 22 , ∠ A M N = 110 ° , ∠ A F M = 70 ° .
Ответы
Ответ:
АЕ = 11 ед.
Пошаговое объяснение:
∠CAM = ∠MAN = ∠NAB = х (дано).
Тогда 3х + ∠В = 90° (1) (сумма острых углов треугольника равна 90°).
В треугольнике АМВ имеем: 2х + ∠В = 180° -110° (2) (сумма внутренних углов треугольника равна 180°).
Вычитаем из (1) (2) и получаем х = 20°.
Следовательно, ∠A = 60°, а ∠В = 30°.
Против угла 30° лежит катет, равный половине гипотенузы.
АС = АВ:2 = 11 ед.
В треугольнике АМF угол ∠MAF = 40° (2х), тогда
∠AMF = 180° - 40° - 70° = 70°.
Таким образом, треугольник MAF - равнобедренный (углы при основании равны) и по свойству равнобедренного треугольника биссектриса АЕ является и высотой, а АМ = AF.
Тогда прямоугольные треугольники АСМ и АЕM равны по гипотенузе и острому углу (АМ - общая, ∠CAM = ∠MAЕ).
Следовательно, АЕ = АС = 11 ед.