Предмет: Математика,
автор: konstantinos057
Памагити. Найти производную в примерах г, е и ж
Приложения:
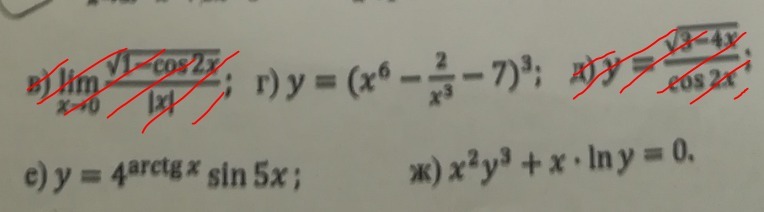
Ответы
Автор ответа:
0
konstantinos057:
Ты настоящий герой
Похожие вопросы
Предмет: Геометрия,
автор: gmimi261
Предмет: История,
автор: katiadrozd426
Предмет: Алгебра,
автор: rodion840
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: smolpro