Предмет: Математика,
автор: DementоR
Вычислить пределы,помогите пожалуйста
Приложения:
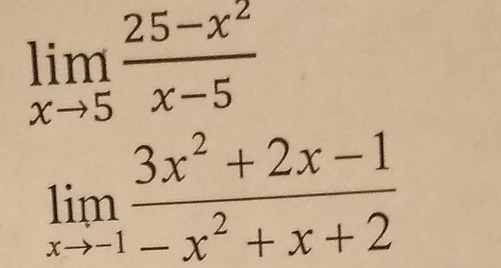
Ответы
Автор ответа:
1
-----------------------------------------------------------------------------
Похожие вопросы
Предмет: Окружающий мир,
автор: varvaraitkool20
Предмет: Математика,
автор: volchanskaya7875
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: ира546
Предмет: Математика,
автор: lopoljg