Question

Найдите пары равных треугольников и докажите их равенство.

Answer 1

НОМЕР 8.
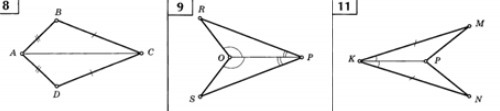
ДАНО: АВ = АD, ВС = CD;
ДОКАЗАТЬ: равенство треугольников ADC и ABС;
Доказательство:
Рассмотрим треугольники ADC и ABC, у них:
AB = AD ( по условию ), BC= CD ( по условию ) и АС - общая сторона. Значит, треугольники равны по трём сторонам или по 3 признаку равенства треугольников.
Ответ: доказано.
НОМЕР 9.
ДАНО: <ROP = <SOP, <RPO = <SPO.
ДОКАЗАТЬ: равенство треугольников ROP и SOP;
Доказательство:
Рассмотрим треугольники ROP и SOP, у них: <RPO = <SPO ( по условию ), <ROP = <SOP ( по условию ) и ОР - общая сторона. Значит, треугольники ROP и SOP равны по двум углам и стороне между ними или по 2 признаку равенства треугольников.
Ответ: доказано.
НОМЕР 11.
ДАНО: KM = KN, <MKP = <NKP;
ДОКАЗАТЬ: равенство треугольников MKP и NKP;
Доказательство:
Рассмотрим треугольники MKP и NKP, у них: KM = KN ( по условию ), <MKP = <NKP ( по условию ) и КР - общая сторона. Значит треугольники MKP и NKP равны по двум сторонам и углу между ними или по 1 признаку равенства треугольников.
Ответ: доказано.